Visualización de Datos Geográficos y Espaciales
En esta unidad veremos visualizaciones que resuelven tareas con datos geográficos y espaciales. Usualmente nos referimos a los mapas con esto, pero también hay datos espaciales que no utilizan mapas. Aquí nos enfocaremos en los datos más comunes, los datos geográficos, que son usualmente visualizados con mapas.
Anteriormente vimos visualizaciones de tablas, lo que nos hace preguntarnos si los datos que se muestran en un mapa también tienen estructura de tabla, donde la posición está almacenada en dos o tres atributos de la tabla. En tal caso, ¿por qué necesitamos otro tipo de representación para resolver tareas con estos datos? Los atributos de posición pueden tener una codificación visual directa, por ejemplo, longitud y latitud a la posición en los ejes x e y. Si hacemos eso, tendremos un mapa.
No es exagerado pensar que todes hemos sido expuestos a mapas en nuestra vida (menos aún si estás leyendo esto en tu teléfono móvil o computador portátil). Los mapas nos son familiares, usualmente sabemos interpretarlos e interactuar con ellos. Sin embargo, eso no quiere decir que no haya desafíos ni codificaciones visuales específicas para cada tipo de tarea.
Podemos encontrar una primera motivación para tratar este tipo de datos y las tareas correspondientes de manera diferenciada en la “primera ley de la geografía,” que dice así:
Todas las cosas están relacionadas entre sí, pero las cosas más próximas en el espacio tienen una relación mayor que las distantes.
– Waldo Tobler
Esta relación de cercanía y dependencia espacial es importante. Tanto así, que para muchos problemas que se resuelven con datos que necesitan tomar en cuenta como la geografía influye en el fenómeno que se esté analizando. Veamos el siguiente ejemplo, una nota en un medio chileno que utiliza un mapa para apoyar e ilustrar el contenido:
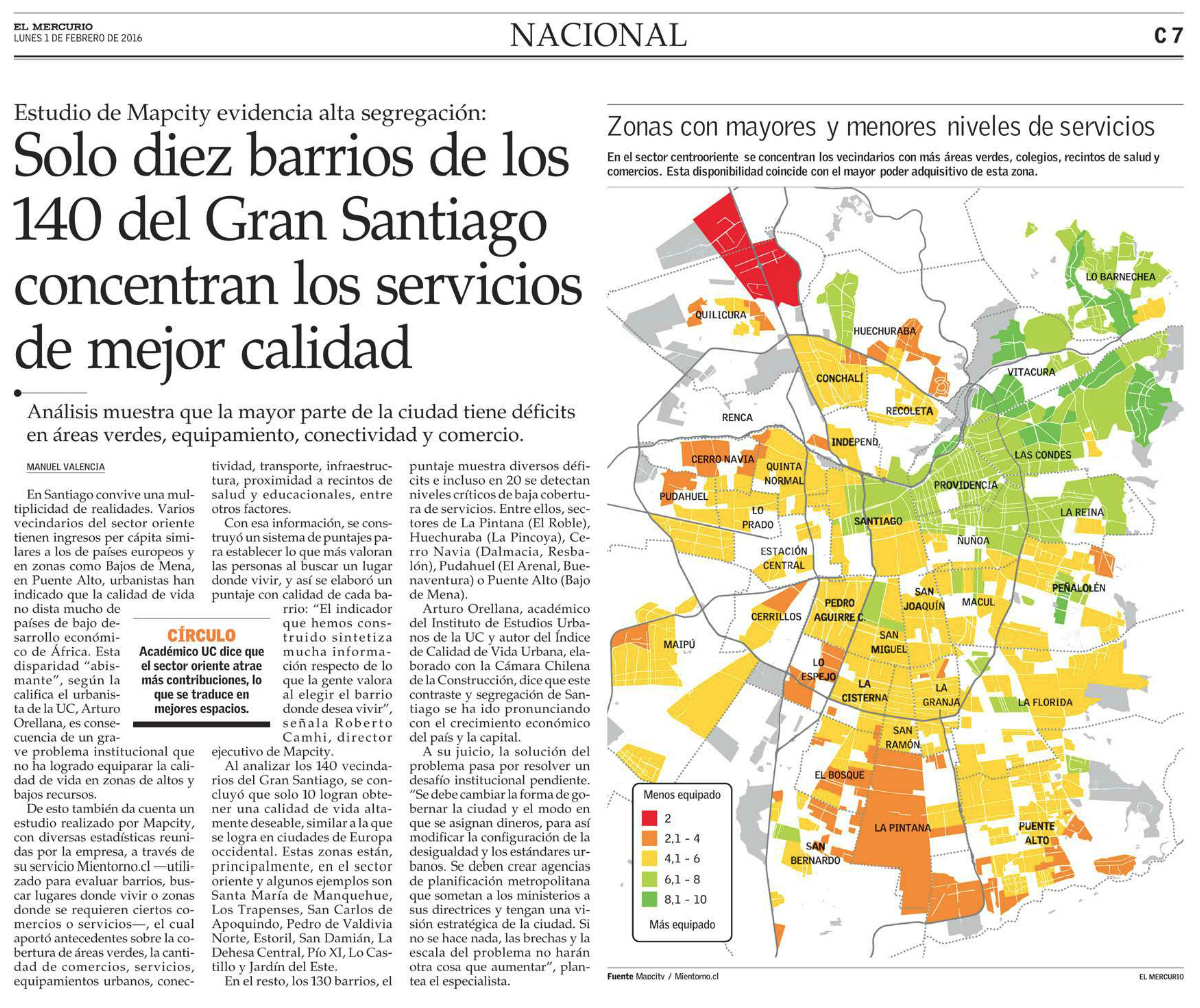
El tipo de visualización que aparece en este artículo se llama choropleth_map y lo veremos en esta unidad. Como adelanto, notamos que el mapa utiliza el canal de tono de color para expresar una variable cuantitativa en cada zona de la ciudad, con una marca por zona: una área poligonal cuyo borde está determinado por límites administrativos o por calles importantes. El titular menciona explícitamente la distribución de los datos, particularmente su extremo superior: “solo diez barrios de los 140 del Gran Santiago concentran los servicios de mejor calidad.” Sin embargo, sin poder ver el mapa, no sabríamos que estos barrios tienden a estar en un sector específico de la ciudad, ni que tienden a ser contiguos. De hecho, el texto del artículo puede llevar a malentendidos: dice “En Santiago convive una multiplicidad de realidades,” cuando en realidad lo que nos muestra el mapa es que estas realidades no conviven — están segregadas, casi separadas de manera quirúrgica por ejes específicos en la ciudad. Una visualización de tablas no nos habría permitido entender ese aspecto de los datos.
Así, en esta unidad veremos distintas tareas y visualizaciones que ponen énfasis en las relaciones espaciales entre los elementos que estemos visualizando. Seguiremos la estructura de la clase de visualización de tablas: identificaremos técnicas específicas para las que comentaremos la codificación visual, las tareas relevantes, y casos de uso.
Hagamos un Ejercicio #
Antes de ver las técnicas, hagamos un ejercicio que puede ser provechoso para nuestro proyecto en el curso. De cierto modo, el proyecto tiene una estructura similar a una nota en un medio: debe contar una historia en un espacio limitado. Una diferencia es que lo principal será visualización (uno o más gráficos), apoyada con texto (anotaciones, notas, títulos, comentarios), y no al revés.
El ejercicio es un pie forzado:
- Bajen un mapa de la ciudad en la que viven. Si viven en Santiago, este mapa en Wikipedia (hagan clic en “versión SVG”) les puede servir. Si no, seguro encontrarán un mapa que esté en blanco en Wikipedia (por supuesto, incluyendo atributos y límites geográficos)
- Impriman ese mapa y cuenten una historia con datos sobre él (también lo pueden hacer en Paint, Gimp, o similares). Los datos tienen que estar en su cabeza e incluso pueden ser inventados. El mapa debe tener un título y contar la historia utilizando elementos gráficos sobre el mapa, incluyendo notas.
- En la clase haremos un documento compartido para revisar los mapas que hayan dibujado. Pueden hacerlo antes o después de leer el resto de esta unidad. Los mapas no serán hechos públicos excepto para el resto de la clase.
Ejemplos de historias que se pueden contar: ¿cuáles son los lugares importantes de la ciudad para mí?¿cuáles son las calles más importantes (según un criterio específico, por ej., las calles con más árboles, las calles con aromas de panadería, etc.)?¿cuáles lugares no conozco y me gustaría conocer, cuáles son sus características?¿dónde creo que viven mis colegas?¿dónde están los portales a otras dimensiones y otras realidades alternativas?
Mapa de Puntos #
El mapa de puntos o dot_map tiene un nombre que lo describe de manera sucinta: es literalmente un mapa con puntos encima. Cada punto (marca) representa a un elemento en el dataset, posicionada en la imagen de acuerdo a sus coordenadas geográficas. Los canales de color se pueden utilizar para expresar atributos de cada una de esas observaciones. El siguiente ejemplo, llamado Mobile Devices + Twitter Use, visualiza millones de tweets publicados en el mundo, cada tweet como un punto, con un color que expresa el tipo de dispositivo que publicó cada mensaje. Se ve así:

Representando los datos (la posición de los tweets) de manera directa podemos resolver tareas de analizar distribución espacial y determinar formas. Por un lado, los puntos grafican calles importantes, áreas que concentran publicaciones, los límites de la ciudad, casi como una vista nocturna desde un avión, con las luminarias dibujando un mapa sobre el terreno. El uso del canal tono para expresar el atributo categórico de dispositivo móvil nos muestra que las distribuciones son distintas para cada dispositivo: el uso de iPhone se concentra en los sectores más ricos de la ciudad (algo esperable dado que es un teléfono más caro que la mayoría de dispositivos Android).
La escalabilidad de un dot_map es grande: podemos mostrar millones de puntos sobre un mapa (¡de hecho eso hace el ejemplo!). A diferencia de un scatterplot, en un dot_map la probabilidad de que los puntos se concentren es alta, permitiéndonos mostrar más, pero fomentando otros problemas también. Por ejemplo, una persona podría interpretar que las áreas predominantemente rojas del mapa (tweets de iPhone) no contienen puntos verdes (tweets de Android). No es así — la sobreposición (overlap) podría ocultar eso.
Mapa de Burbujas #
El bubble_map extiende la codificación visual del dot_map, al utilizar el canal de tamaño en cada punto para crear burbujas de tamaños variables. Lo consideramos una visualización distinta porque el uso de ese canal implica que la escalabilidad y las tareas que puede resolver la visualización cambian. Por ejemplo, ya se vuelve difícil determinar la forma específica de las áreas de interés, por lo que usualmente se agrega información auxiliar. El siguiente gráfico es un bubble_map que muestra los terremotos asociado a la Placa de Nazca entre los años 1900–2016:
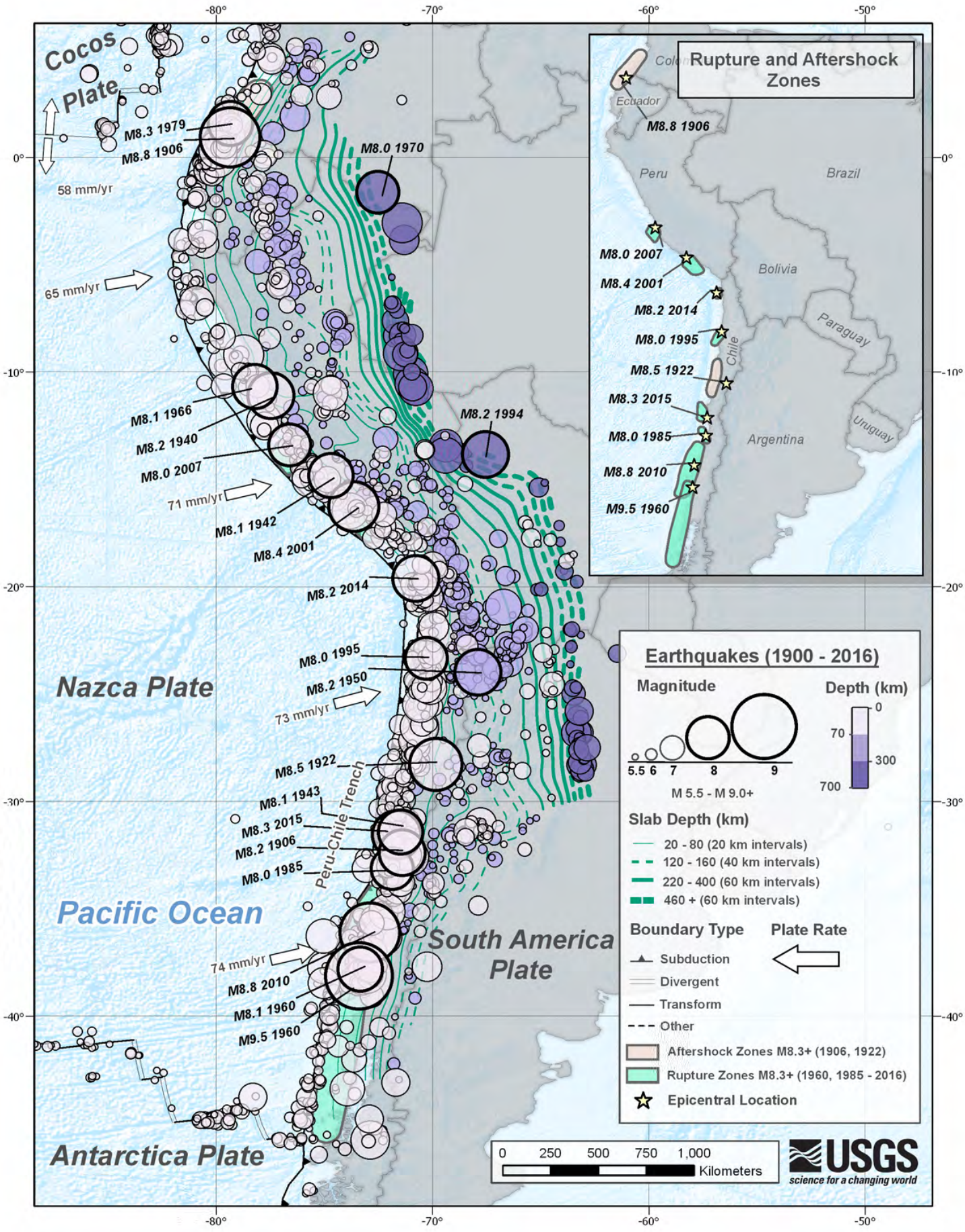
La tarea que resuelve esta visualización es buscar dónde se encuentran los elementos que cumplen un criterio específico, o bien, explorar las características de un lugar en función de lo que se está mostrando, o identificar tendencias en la geografía. Su escalabilidad es menor debido a la sobreposición de las burbujas y al tamaño de éstas. El gráfico de ejemplo de la USGS muestra centenas de terremotos, no miles ni millones de ellos.
Cuando vimos codificación visual aprendimos que el área de un círculo no es un buen canal para comparar magnitudes. Sin embargo, de los canales que tenemos disponibles, y de acuerdo a la tarea que tengamos que resolver, en un bubble_map es aceptable usar este canal para comparar tamaño, si lo que queremos es enfatizar que una burbuja es más grande que otra, pero no por cuánto.
Usualmente en un bubble_map se trabaja con tablas donde la unidad de análisis o elementos son agregados o abarcan un área extensa, en contraste con el dot_map, donde los elementos podían ser tan detallados. Veamos dos ejemplos. En el primero se visualizan los orígenes y destinos de viajes en transporte público en Santiago. Los viajes fueron agrupados por zona de origen y zona de destino, de modo que se puede contar cuál es la cantidad de viajes se inicia o que termina en cada zona. Cada burbuja se posiciona en el punto central (o centroide) de la zona correspondiente:
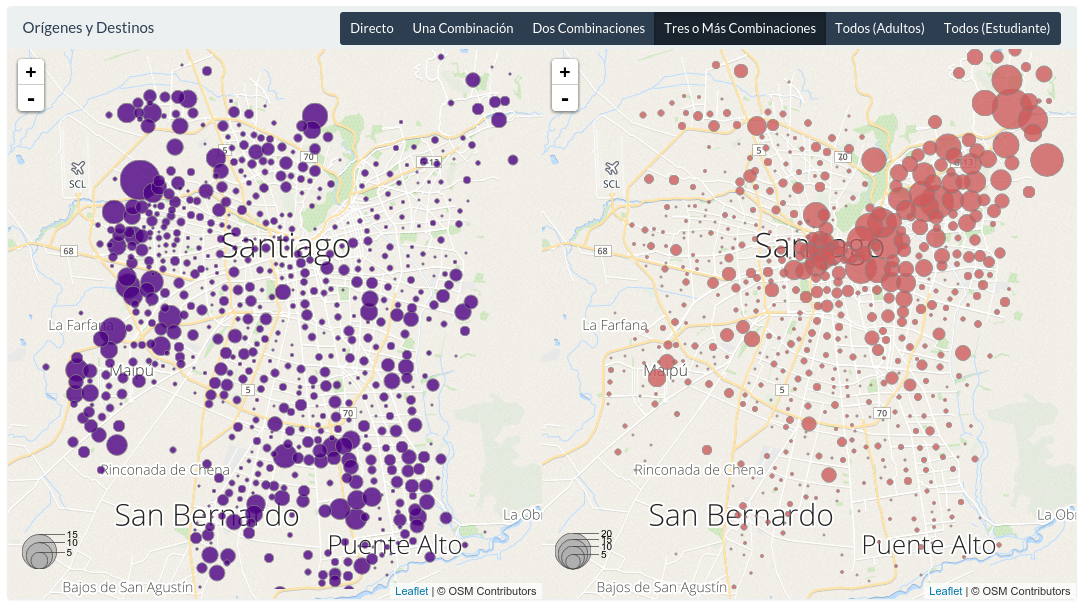
Estas visualizaciones nos muestran que cierto tipo de viajes (de tres combinaciones) se concentran en las zonas periféricas de la ciudad, y generalmente todos ellos se dirigen al sector centro-oriente de Santiago. También nos dice que cuando hay una burbuja grande, las burbujas alrededor también suelen ser grandes — la visualización exhibe las relaciones espaciales en los datos de manera efectiva.
El mapa anterior utiliza una burbuja por zona, sin embargo, no muestra los bordes de cada una. Eso puede ser un problema si no estamos familiarizados con la geografía o no se muestra información auxiliar, como las calles. Otra manera de atacar el problema es definiendo una grilla regular, y posicionar cada burbuja en el centroide de cada rectángulo. La grilla sigue sin mostrarse, pero su estructura es explícita al ver los centros de las burbujas alineadas. La siguiente visualización proveniente de un estudio de brechas de género en la movilidad aprovecha esta situación para juxtaponer un bubble_map y un dot_map. El bubble_map nos indica si una zona (o celda de la grilla) es más rica o más pobre el resto, y para ello utiliza los canales de tamaño y tono. El dot_map utiliza el canal de saturación de cada punto, que también representa el centroide de cada celda, para indicar si hay una brecha de movilidad, es decir, si las mujeres se mueven menos de lo esperado en comparación con los hombres:
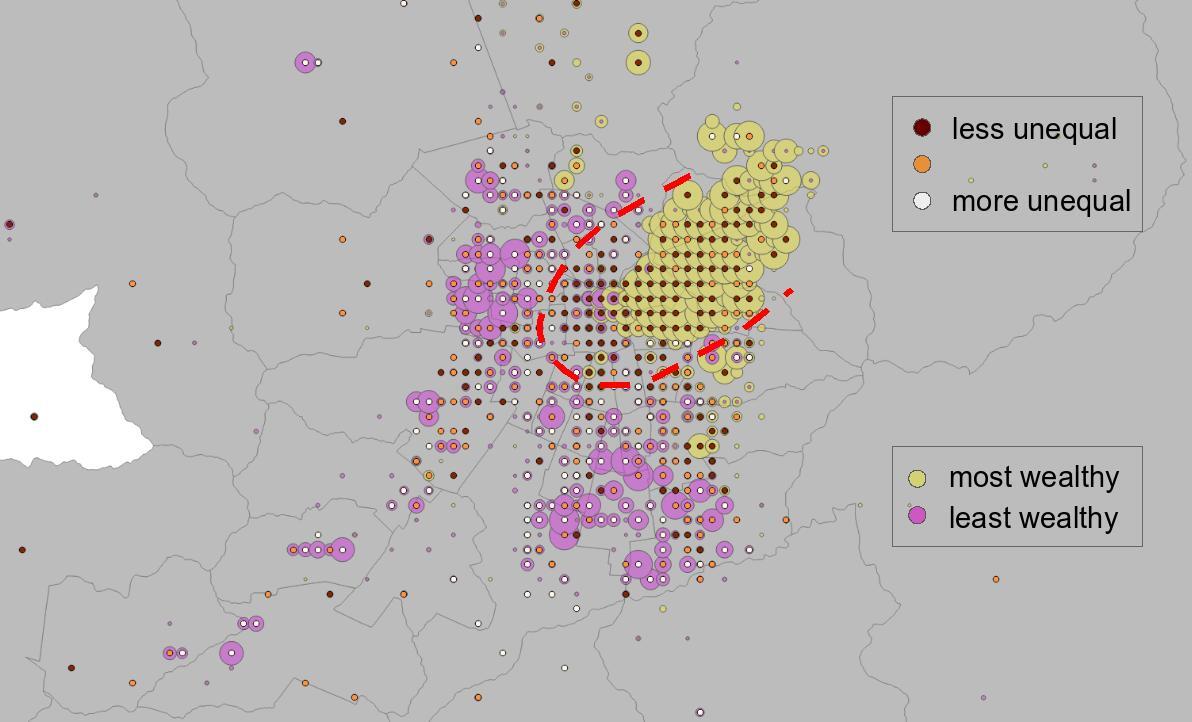
Esta configuración nos permite fijarnos en dos variables a la vez, y dar contexto socio-económico al fenómeno bajo análisis: la brecha de género.
Volveremos a hablar del bubble_map luego de revisar el siguiente tipo de visualización.
Mapa de Coropletas #
El choropleth_map es otra de las visualizaciones clásicas de datos geográficos, cuyo foco son las áreas que se están visualizando, a diferencia de las dos visualizaciones anteriores se enfocaban en las posiciones. Así, el choropleth_map nos permite encontrar patrones espaciales en las distribuciones de una variable en el espacio, identificar outliers espaciales, y también buscar relaciones con otras variables. El mecanismo para hacerlo es desplegar directamente las áreas de los datos como marcas (por ej., manzanas, distritos, comunas, regiones, países), utilizando el canal de saturación o de luminosidad para expresar valores ordinales o cuantitativos. El siguiente ejemplo muestra cuántas vidas hemos perdido en el planeta durante la pandemia de COVID-19 en asociación al virus:
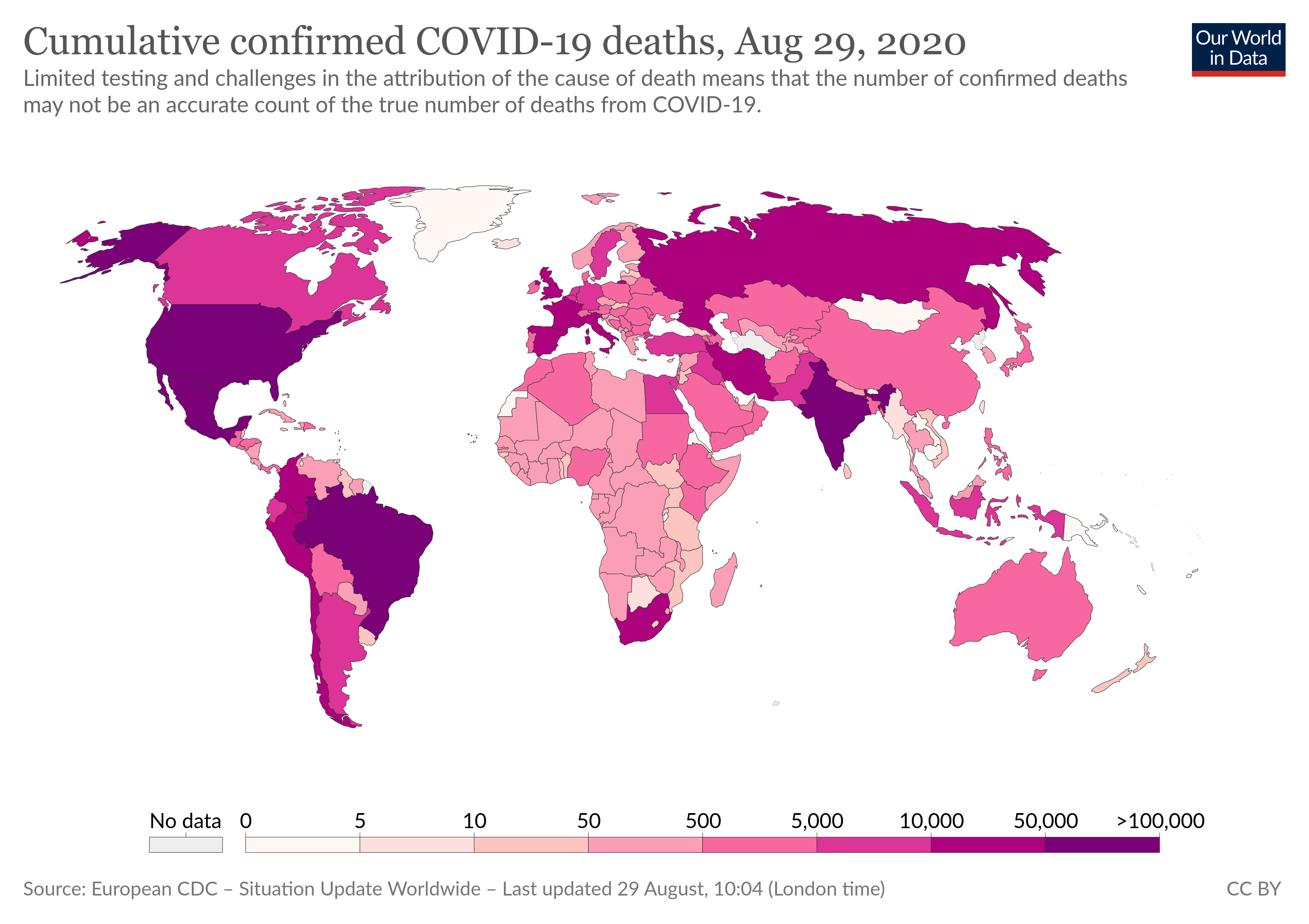
Como vemos en la leyenda, este choropleth_map utiliza cada país como una marca de manera directa, expresando el total de muertes a través del canal de saturación, donde cada color representa valores dentro de un rango específico. Ahora bien, al ser un valor total por país, debemos preguntarnos si la magnitud que estamos expresando es el valor adecuado. ¿Por qué? Porque ese valor está correlacionado con la población de un país, y por tanto las conclusiones que saquemos de la visualización estarán considerando ambas magnitudes sin que nos demos cuenta.
Para resolver el problema podemos utilizar un valor relativo, por ejemplo, la tasa de muertes por un millón de habitantes:
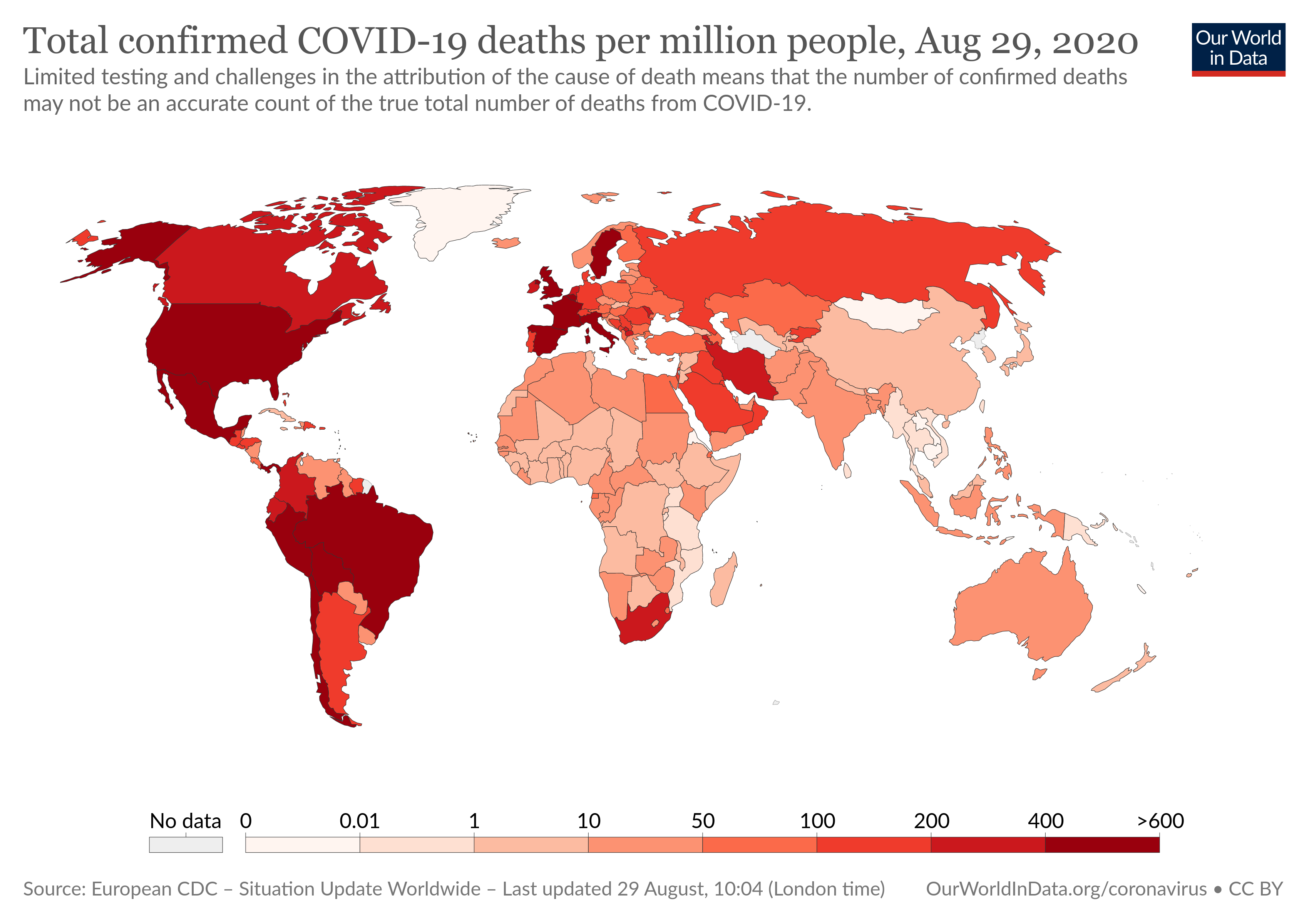
Al usar una tasa podemos realizar comparaciones de manera efectiva. Observen que algunos países cambiaron de ranking en el gráfico: algunos que eran más oscuros que los demás ahora son más claros, y viceversa.
Veamos un ejemplo a una escala más pequeña. El siguiente mapa de Santiago ilustra el nivel socio-económico de cada cuadra (o bloque o manzana) de Santiago:

Al igual que en los gráficos anteriores, este choropleth_map utiliza la saturación para indicar mayores valores en un atributo, esta vez ordinal. Además, se complementa el gráfico con un dot_map que contiene supermercados (grandes, no los de conveniencia, a pesar de que también puedan llamarse así), y también líneas que nos indican las posiciones y extensiones de ferias libres (mercados al aire libre que se instalan en las calles uno o dos días a la semana). Esto permite ver una posible relación entre nivel socio-económico predominante de una manzana y sus alrededores, y las maneras de abastecimiento a las que tiene acceso.
Algo que no discutimos es cómo elegir la cantidad de rangos o niveles a visualizar, ni como elegir sus límites. En los atributos ordinales esto puede no ser un problema, pero en los atributos cuantitativos puede prestarse para percepciones erróneas. En los ejemplos que hemos visto no discutimos cómo elegir la cantidad de niveles, ya que es una decisión de diseño dependiente de la tarea a resolver y de la estructura de los datos. Veremos ese tema en la clase práctica, donde exploraremos cómo la biblioteca de análisis espacial mapclassify provee herramientas para determinar los niveles y sus extensiones.
En general, un choropleth_map visualiza atributos cuantitativos, pero también se puede utilizar un atributo categórico. En dichos casos es difícil elegir una buena paleta de colores si son muchas categorías.
Por último, una advertencia: en la clase de codificación visual hablamos de separabilidad e integridad de canales. El tamaño del área influye en la percepción del color. Debido a esta interferencia un color oscuro (usualmente mayor magnitud) en un área pequeña puede ser ignorado en favor de un color más claro (usualmente menor magnitud) en un área más grande.
Consideraciones para elegir entre dot_map, bubble_map y choropleth_map #
Las tres visualizaciones que hemos visto funcionan para tareas distintas, pero, de manera similar a como hablamos antes de bar_chart y line_chart, se pueden usar de manera intercambiable — y podemos estar cometiendo errores al hacerlo. Para ejemplificar esta situación revisemos el que posiblemente es el choropleth_map más difundido de la historia. Corrresponde a una visualización de los condados de Estados Unidos en los que ganó Donald Trump el año 2016, en una versión publicada en la introducción del libro How Charts Lie:
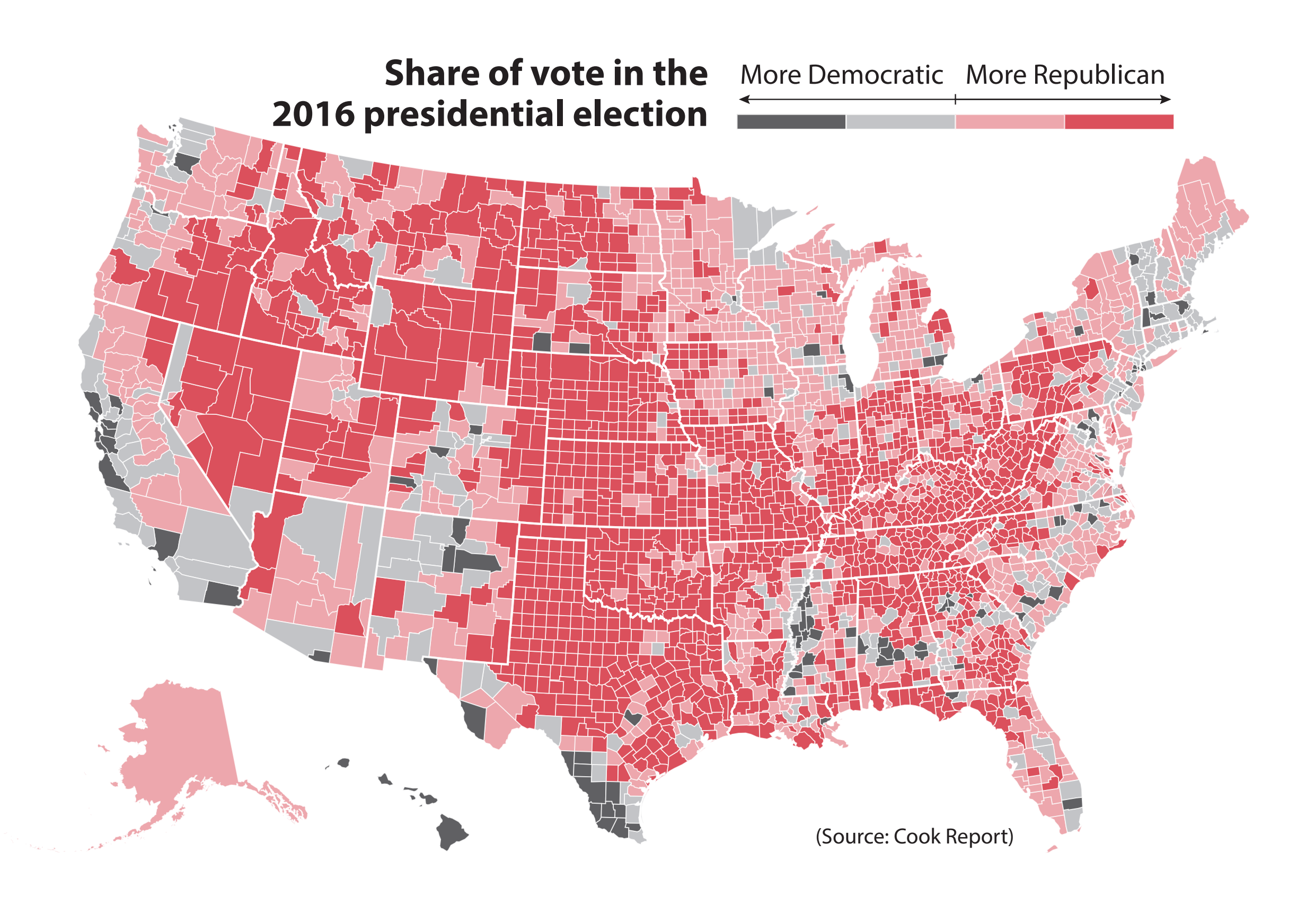
Una versión de este mapa fue exhibida por Trump en Twitter como un argumento a favor de su popularidad en el país. Fue también exhibido en la Casa Blanca en reuniones oficiales. Trump se lo enseñó al presidente de China, Xi Jinping, diciendo algo como “mira esto, éste es el mapa con los resultados finales. Está muy bien, ¿cierto? Obviamente nosotros somos el color rojo.”
Si miramos las estadísticas de las elecciones de ese año en los EEUU, veremos que Hillary Clinton obtuvo más votos que Trump, pero no ganó debido a que no obtuvo los votos suficientes de los electores (recuerden que en EEUU una persona vota por un representante en el colegio electoral, no directamente por les candidates). Entonces, ¿cómo es posible que la mayor parte del país se vea de color rojo (que es asociado al Partido Republicano)? La respuesta la encontramos en el siguiente dot_map creado por Kenneth Field, donde cada votante es representando con un punto, cuyo color expresa el partido al que pertenece el votante:

Este mapa aclara la situación: la densidad poblacional de cada condado no es igual. Gran parte de los condados rojos en el primer mapa tienen una densidad de población baja, sin embargo, acaparan gran parte de la superficie del país.
Así, lo que visualiza el choroplet_map es el territorio, no a las personas. Además, noten que expresar cuál partido ha ganado no es lo mismo que expresar la proporción de los votos obtenidos. La variable que se decide expresar altera el significado y la interpretación de la visualización, por sutil que parezca la decisión.
El dot_map tiene limitaciones, a fin de cuentas sí nos interesa la distribución de los votos por unidad territorial (condados), no los votos de cada persona. Un bubble_map nos permite expresar este resultado, al contar la proporción del total de votos en cada condado que recibió el partido ganador correspondiente:
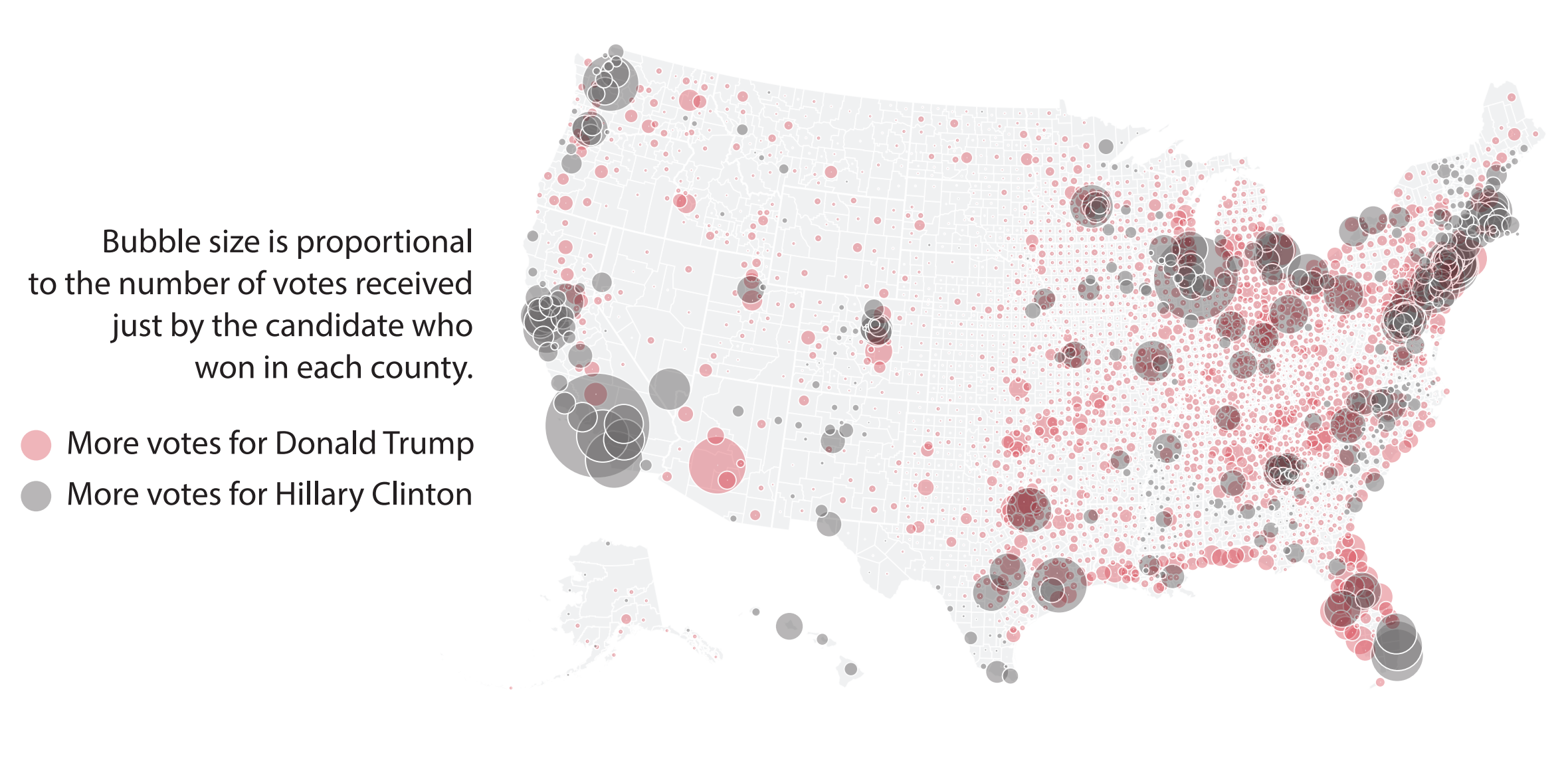
Aquí observamos que efectivamente hay más condados donde ganó Trump, pero que Hillary ganó en áreas donde obtuvo más votos. Ahora bien, este mapa también debe ser interpretado con cuidado: noten que estamos mostrando la proporción del total del partido ganador en cada condado. ¿Qué pasa con los votos del partido perdedor en cada condado? No se despliegan, lo que, junto al gran tamaño de las burbujas grises, puede llevar a sobredimensionar la cantidad de votos que obtuvo Hillary Clinton. Una solución a este problema es mostrar los votos de cada partido en todos los condados, permitiendo expresar el total de los votos. Para evitar la sobreposición, se pueden utilizar dos mapas en paralelo:
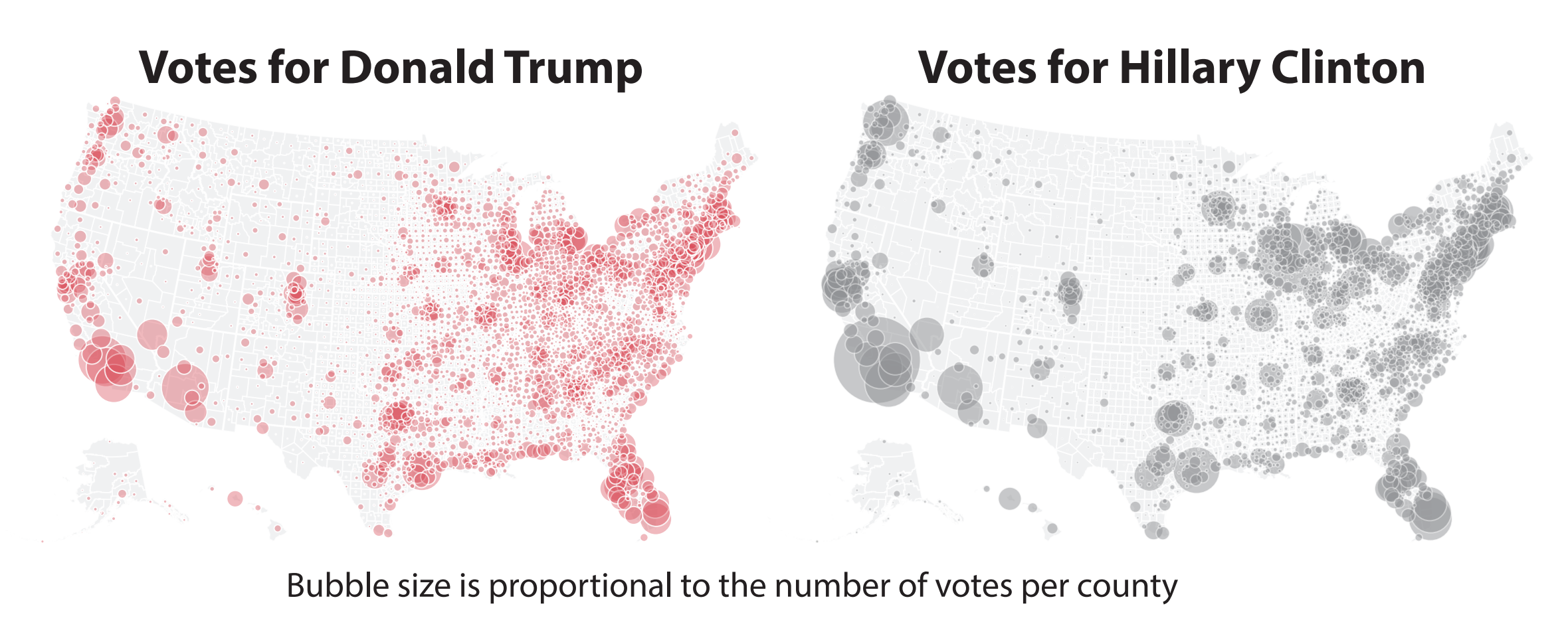
¿Qué les parece este mapa? Nos permite entender los patrones detrás de los votos que recibió cada candidate. No podremos calcular el total exacto de votos (estamos utilizando áreas para comparar magnitudes), pero sí podremos comprender la distribución territorial de los votos y la concentración de éstos.
El libro How Charts Lie cuenta esta historia y muchas otras, que nos ayudarán a aprender a reconocer cuándo un gráfico puede ser malinterpretado, y como podemos evitar caer en esos errores, tanto como diseñadores como usuaries de una visualización.
Ninguna de estas visualizaciones es mejor que las otras per se. Algunas son mejores que otras para ciertas tareas y para cierto tipo de datos, como hemos comentado antes. Utilizar la visualización que no es adecuada para la tarea puede llevar a errores, aunque la mayoría de las las decisiones de diseño que llevan a las interpretaciones erróneas no tengan ese propósito. Algunas sí la tienen — y debemos estar preparades para identificar y actuar ante esas situaciones.
Heatmap #
Un heat_map define a una familia de visualizaciones que comparte nombre con una visualización para tablas porque el propósito es similar: representar zonas calientes y frías en los datos (para distintas definiciones de ambos términos). Al trabajar con una tabla, nos referíamos a grupos de filas y de columnas en la tabla; en el caso de datos espaciales, nos referimos a lugares. Hay dos maneras de hacer un heat_map: contar la cantidad, intensidad o peso de un atributo en una posición o área específica; o bien derivar los límites de zonas con mayor peso que otras.
En el primer grupo están variantes de las visualizaciones que ya hemos visto. Por ejemplo, en un heat_map de puntos, utilizamos el canal de luminosidad de modo que, cuando dos o más puntos se sobreponen, la luminosidad de éstos se suma. El siguiente gráfico creado por Facebook llamado Visualizing Friendships utiliza ese concepto para mostrar la popularidad de Facebook. Al igual que en un dot_map, la densidad y color de los puntos delimitan los bordes de países y continentes:
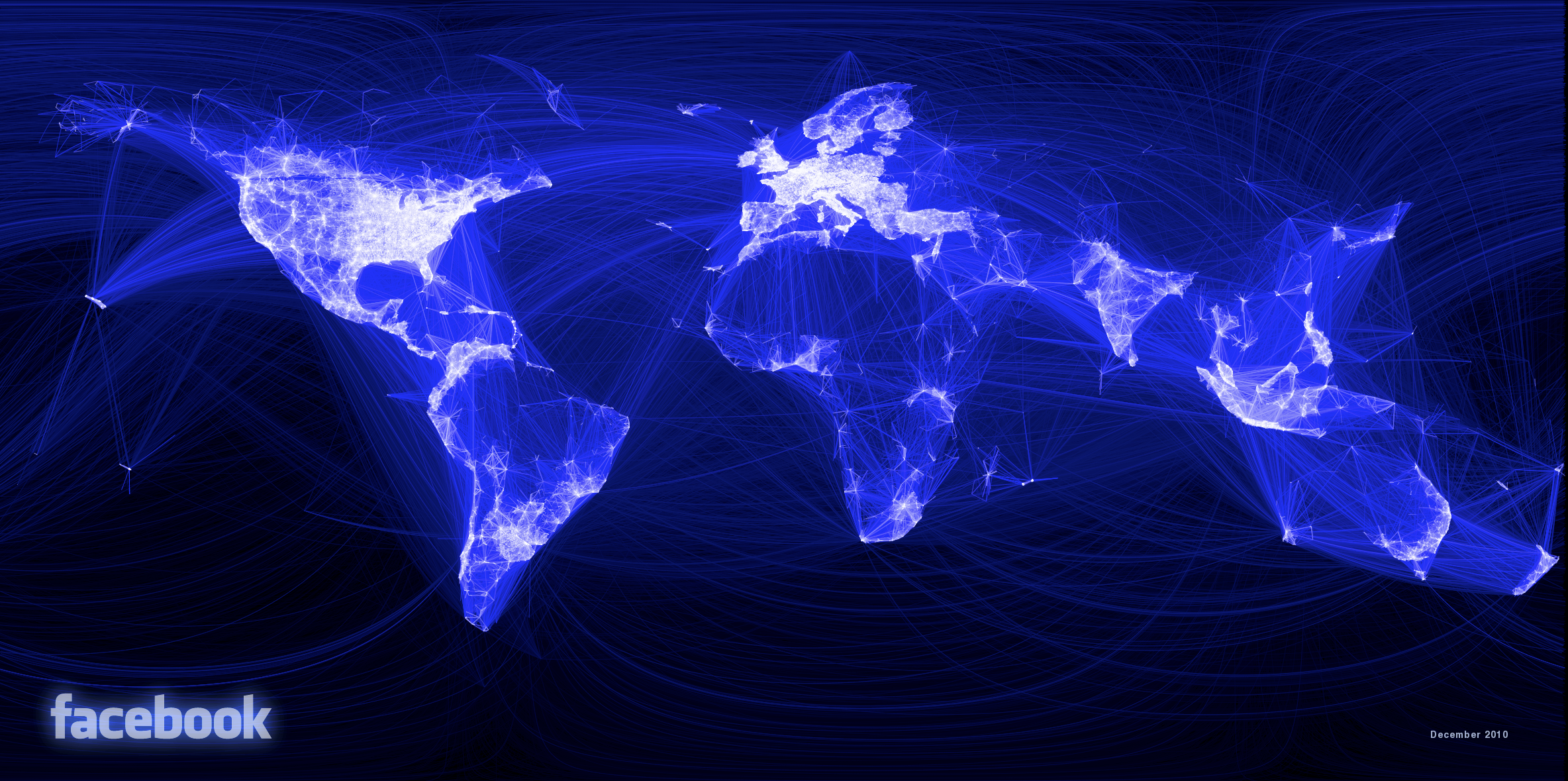
Adicionalmente el mapa contiene líneas que representan las amistades en Facebook. Cada línea es representada como un arco por dos motivos: primero, reduce el problema de la sobreposición; segundo, en nuestro planeta la curva más corta que conecta dos puntos tiene una representación de arco en un mapa como éste, debido al haber “aplanado” el mundo a través de una proyección. De esto hablamos al final de esta unidad.
Un heat_map también se puede aplicar sobre líneas o trayectorias. El siguiente mapa utiliza de la misma manera el canal de luminosidad, pero las marcas son líneas en vez de puntos. Las líneas representan las trayectorias frecuentes de usuaries de Strava, una aplicación de registro de viajes deportivos (bicicleta, hiking, trote, etc.):
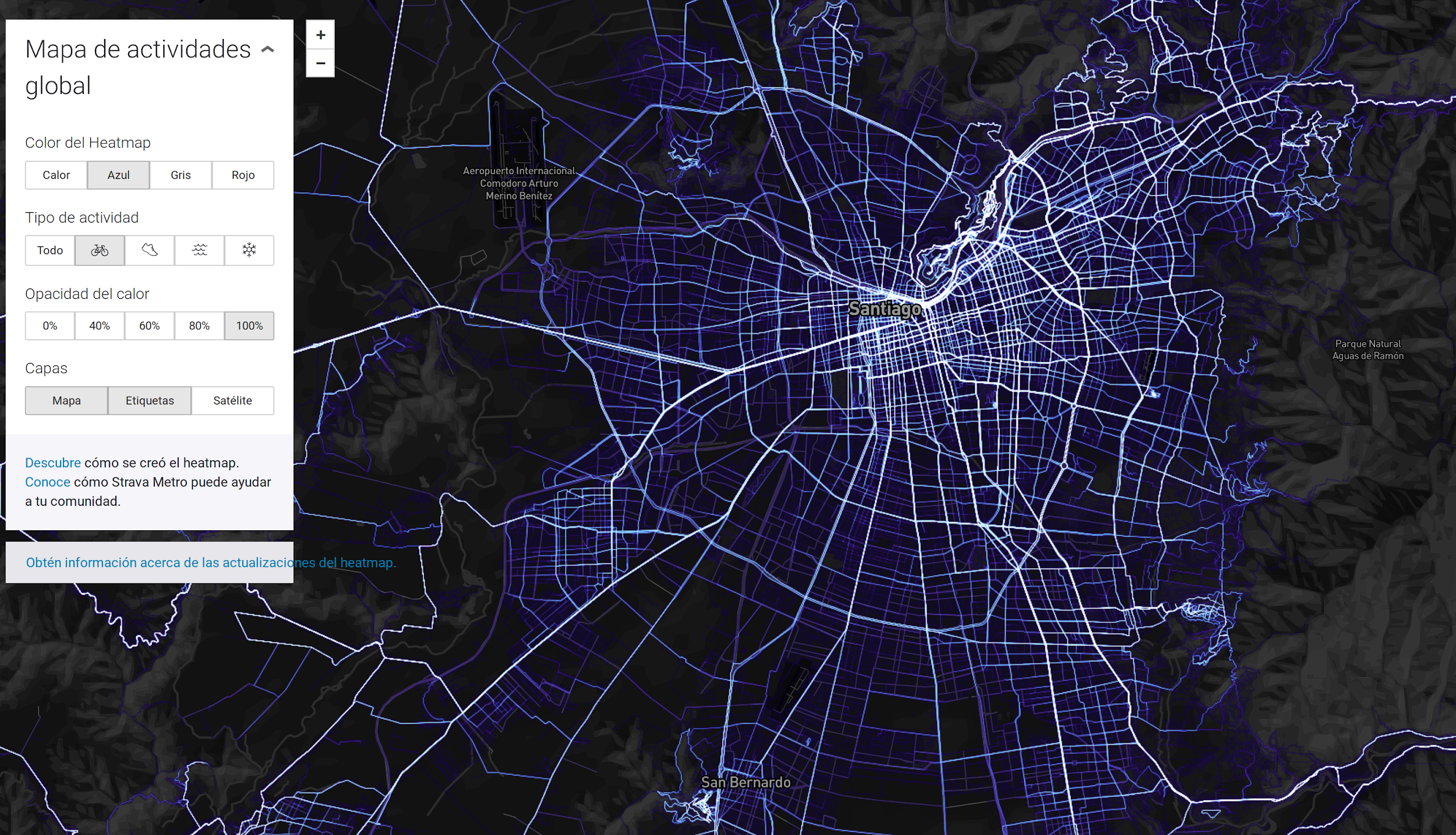
El efecto es el mismo. Podemos ver dónde se utiliza la bicicleta en la ciudad. Es una visualización efectiva para determinar la distribución espacial de una variable, para encontrar tendencias respecto a las zonas que son más (o menos) representativas de ésta.
Cuando un heat_map se hace sobre áreas se suele utilizar una grilla. El siguiente ejemplo muestra la presencia de una especie de aves migratorias (golondrinas en este caso) en América:
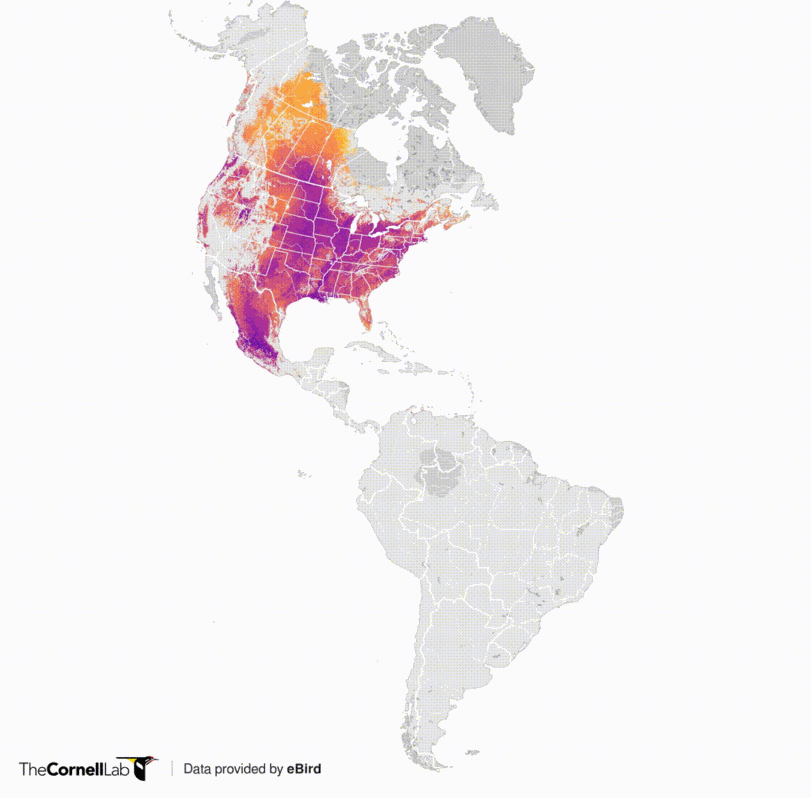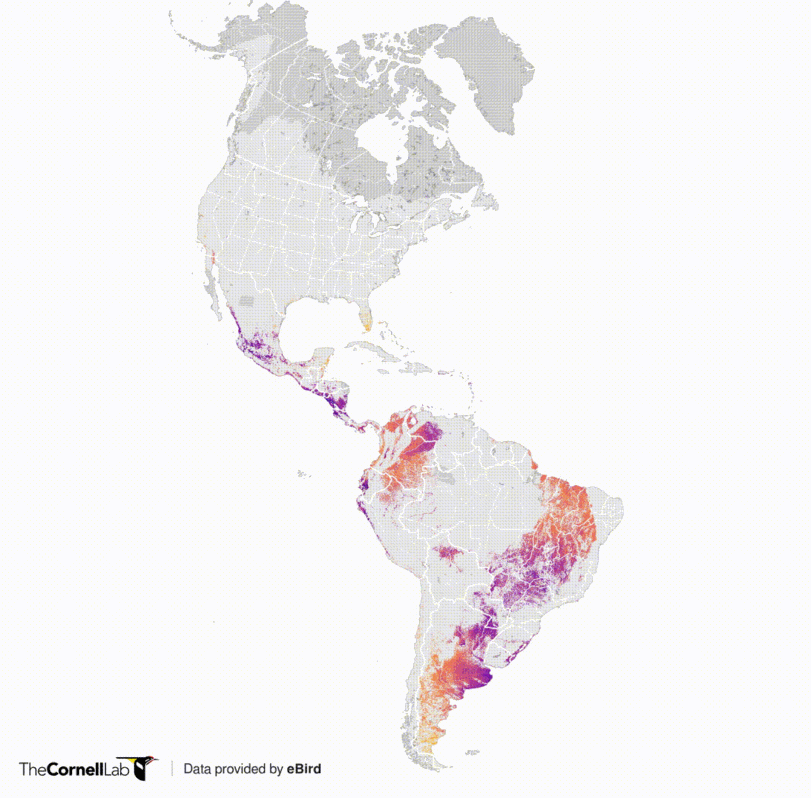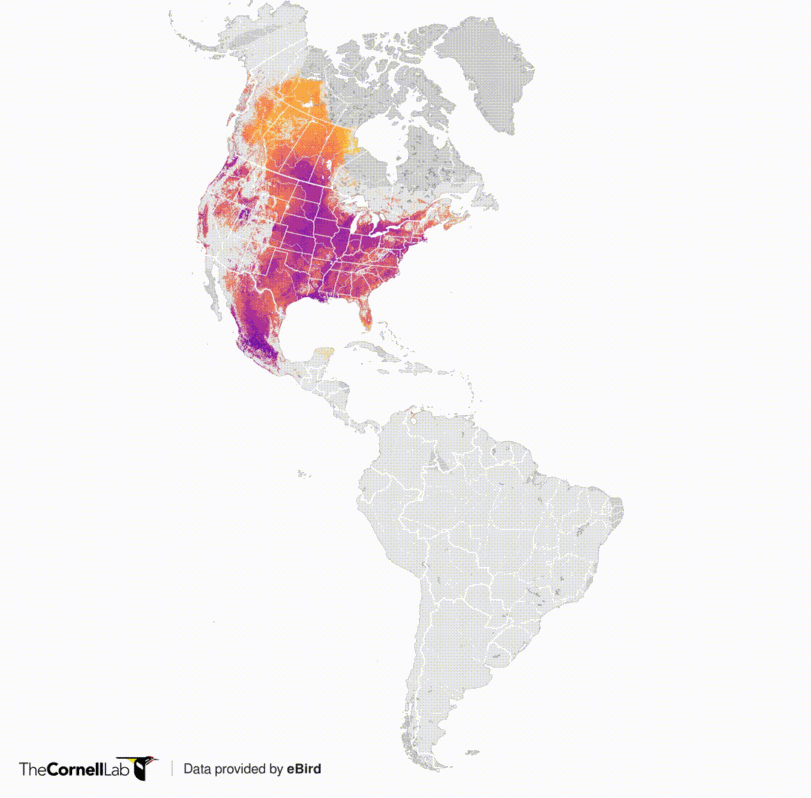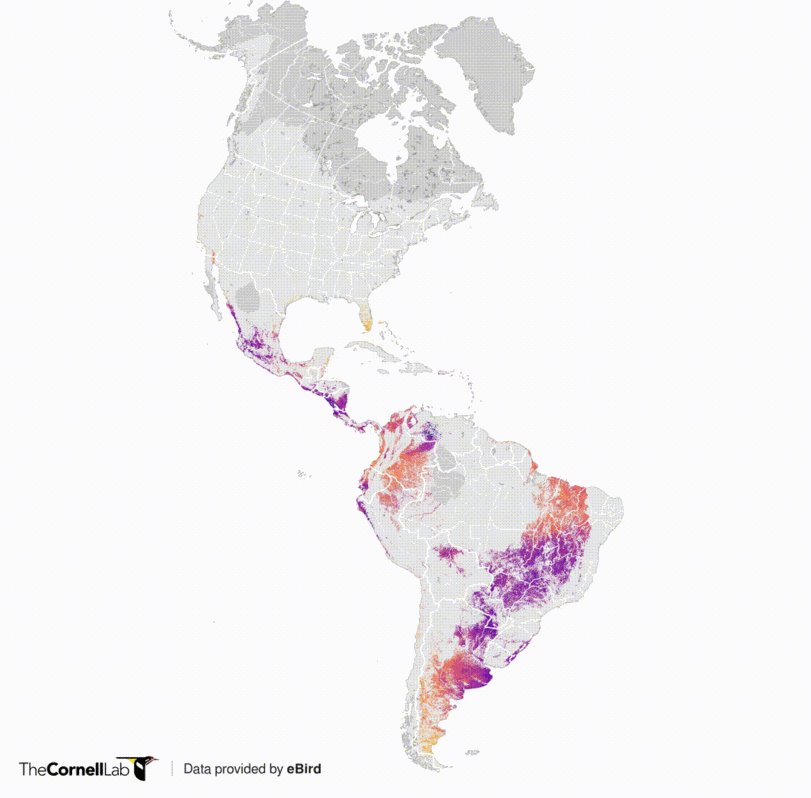
La versión animada nos permite ver como varía la distribución en el tiempo dado el patrón de migración de las golondrinas. La unidad de análisis es una celda de en celdas de 2,96 kilómetros de ancho. Dada la escala del mapa, estas celdas parecen puntos, pero no lo son: son áreas cuadradas.
En los tres heat_map anteriores la unidad de análisis era la unidad de agregación (puntos, líneas, áreas). El segundo estilo de heat_map toma los datos originales, que usualmente está compuesto por puntos, y deriva una nueva geometría que representa las zonas de alta (o baja) intensidad de una variable de interés. Para esto se pueden utilizar técnicas como Kernel Density Estimation — tal como en una dimensión KDE nos permite obtener una distribución, en 2D también. El siguiente mapa ejemplifica esto, al tener como unidad de análisis las manzanas de Santiago, y derivar zonas de déficit habitacional (heat_map de tonalidad azul) y zonas de concentración de proyectos inmobiliarios (heat_map de tonalidad roja):
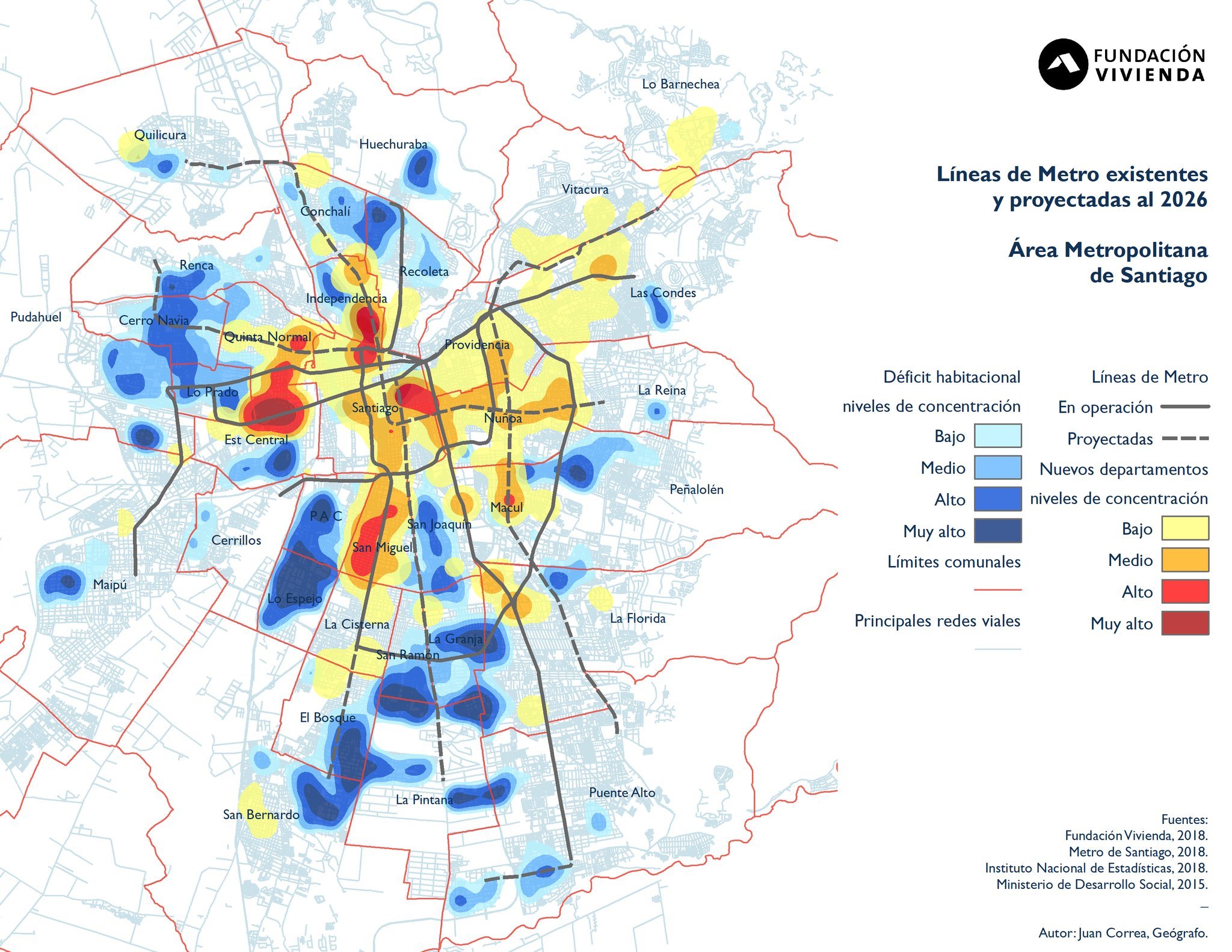
Así, el heat_map nos permite entender la distribución espacial de esas variables, y, al mismo tiempo, al mostrar dos variables distintas podemos ver cómo estás se relacionan en el espacio. Los marcadores de líneas de metro también nos ayudan a interpretar el resultado.
Al igual que en el choropleth_map, en este tipo de heat_map tenemos que decidir los rangos de los niveles. Adicionalmente, tenemos que configurar los parámetros de la KDE (como el bandwidth). La visualización que obtengamos dependerá de esos parámetros.
Contour Maps #
Un contour_mapcomparte parte de la codificación visual del heat_map que deriva áreas de intensidad alta (o baja). Sin embargo, tiene diferencias a nivel del tipo de dato, ya que se trabaja con un campo escalar cuantitativo sobre la geometría, y a nivel de tarea, ya que se busca encontrar las áreas cuyo contorno tenga un valor específico. Veamos un ejemplo de contour_map que visualiza las islas de calor en Santiago:

Esta nota nos muestra los lugares de Santiago cuya temperatura (campo escalar) sobrepasa ciertos umbrales (36°C, 38°C, 40°C, 42°C, 44°C), determinados antes de realizar la visualización, puesto que sabemos que son relevantes para la tarea. Los contornos son líneas derivadas del campo escalar en los que el valor del campo es constante. Por ello, se denominan isolíneas.
Posiblemente el tipo de mapa de contornos más común es el topographic_map o mapa topográfico:
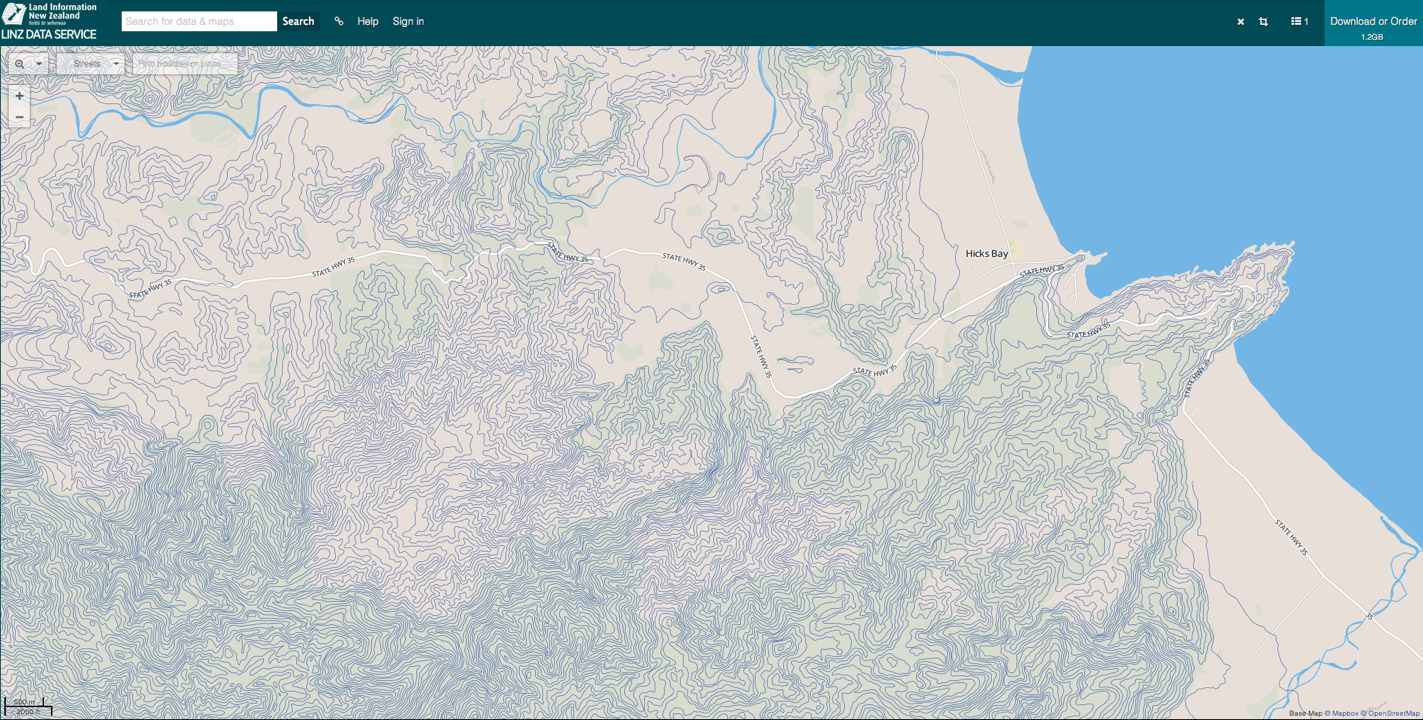
En un mapa topográfico, distintos niveles de la altura del territorio son expresados con contornos.
Otra especialización de un contour_map son las llamadas isocronas o isochrones, áreas derivadas alrededor de un punto de origen que expresan hasta dónde se puede llegar en un tiempo específico — el campo escalar depende de un punto de referencia en el mapa. Las isochrones permiten responder una pregunta clave en el análisis de accesibilidad a servicios y amenidades en una ciudad: ¿hasta dónde puedo llegar en 15 minutos desde mi hogar? Un lugar que tenga mejor accesibilidad proveerá mejor accesibilidad a sus habitantes. Así, las isochrones permiten visualizar la accesibilidad de un lugar. El sistema COAXS es un ejemplo de dicha visualización, al permitir comparar la accesibilidad actual de un lugar con la accesibilidad post-implementación de una medida urbana, como puede ser la construcción de una línea de metro:
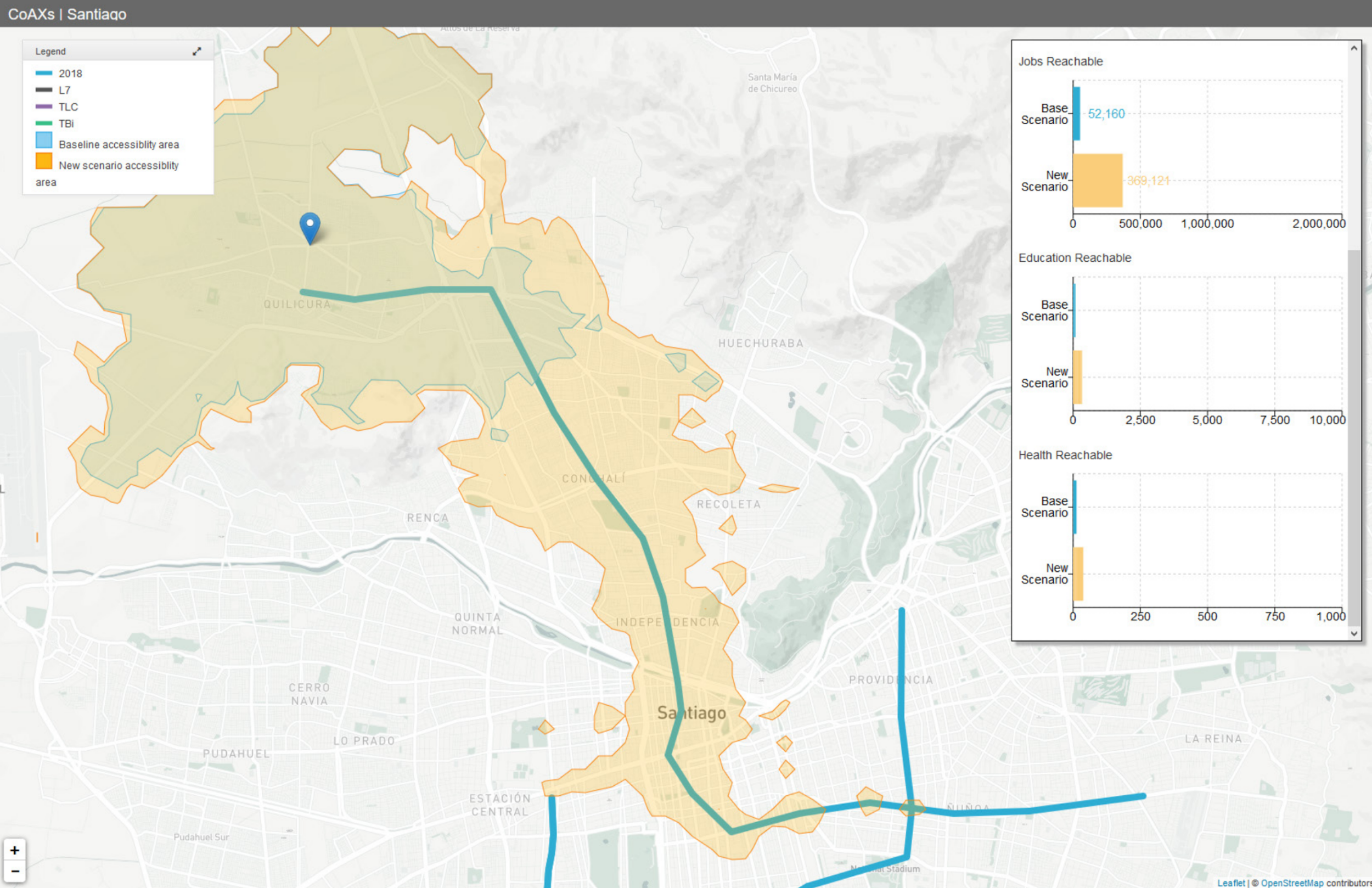
En el ejemplo se compara la accesibilidad en 15 minutos desde el centro de Quilicura en la situación actual y en la situación futura post-inauguración de la línea 7 del Metro de Santiago. ¡Qué cambio!
Flow Maps #
Hasta este momento hemos trabajado con unidades espaciales que tienen una única posición. Sin embargo, el movimiento geográfico es importante, y hoy, quizás, más relevante que nunca — un movimiento que abarca más que personas, ya que también podemos hablar de bienes, de dinero, o incluso de ideas y conocimiento. Los mapas de flujo o flow_map nos permiten ver esas relaciones.
La manera más directa y sencilla de representar flujos de movimiento es a través del origen y del destino del movimiento (dos atributos geográficos) y un atributo cuantitativo (de intensidad, importancia o peso del flujo). Las líneas que unen origen y destino se pueden graficar directamente, con algunas propiedades gráficas que permitan identificar su dirección (una flecha, por ejemplo). Su grosor o color (o ambos canales) puede representar su intensidad. El siguiente flow_map permite ver los flujos de movimiento de personas en Santiago en la hora peak del lunes 9 de marzo de 2020, antes de que la pandemia de COVID-19 llegase a Chile:

Esta visualización interactiva, creada con la herramienta flowmap.blue toma varios resguardos para poder visualizar los flujos y evitar los problemas de sobreposición: utiliza transparencia en los flujos con menor importancia, además del grosor y color de la línea, y grafica los flujos en orden de importancia, de modo que los más importantes se grafiquen al final y por tanto sean visibles (se dibujan encima de los demás). Las tareas que permite resolver esta visualización tienen relación con la distribución espacial de orígenes y destinos, pero también con tareas propias de una red (de hecho, los flujos se pueden interpretar como una red), como encontrar orígenes o destinos importantes, o el camino entre un punto y otro.
Quizás uno de los mapas de flujo de Santiago más conocidos proviene de la Tesis de Irene Molina, de 1985. Es una visualización hecha a mano sobre erradicación de campamentos (flujo de personas) durante la dictadura:
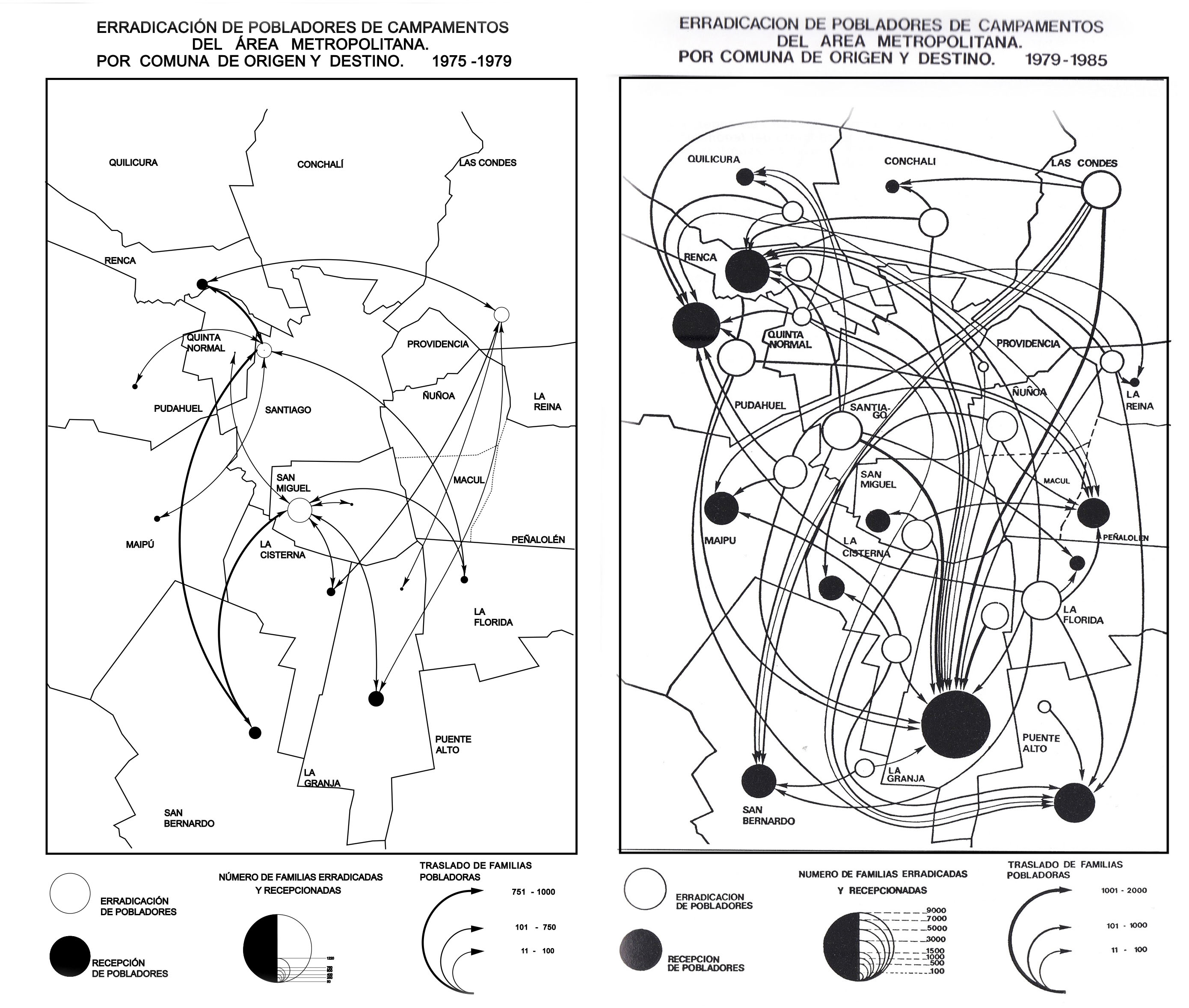
En los dos flow_map que hemos visto, notamos que los orígenes y destinos usan un bubble_map auxiliar para mostrar su importancia en función de la cantidad de flujos que entran y salen de cada punto. Son dos visualizaciones que se complementan bien.
Una versión avanzada de flow_map deriva flujos agregados, que se pueden mostrar como flujos unificados en la visualización. Esta técnica es conocida como flow_map_layout. Al analizar las ramificaciones y trayectorias que siguen los flujos es posible minimizar el largo del total de distancia recorrida por las líneas de flujo, y al mismo tiempo evitar sobreponerse o colisionar con la geografía relevante:
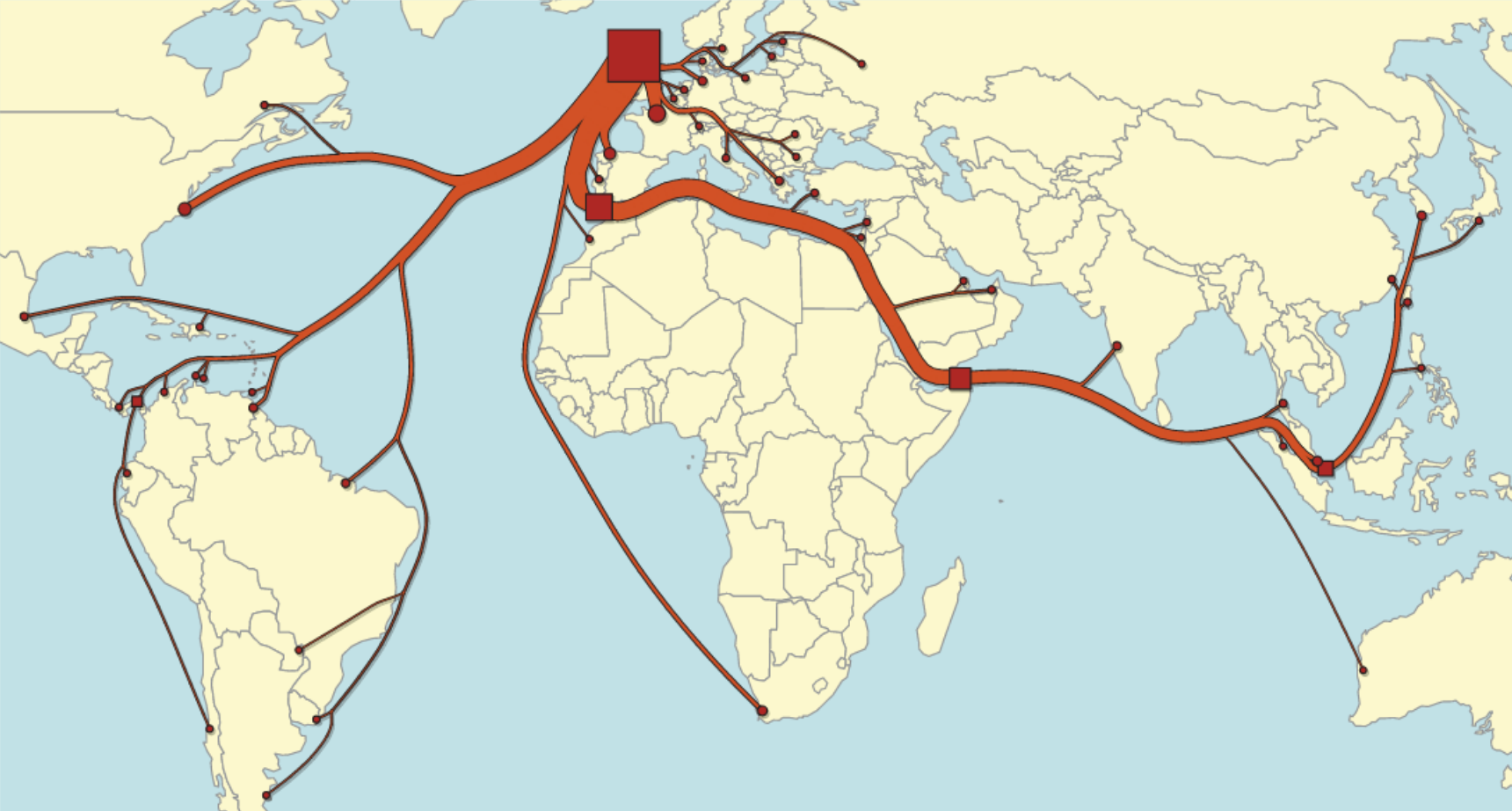
Aunque es un desafío implementar flow_map_layout, existen visualizaciones que toman algunas de sus premisas. La siguiente es una de ellas, parte del artículo interactivo Billions of Birds Migrate.Where Do They Go?:
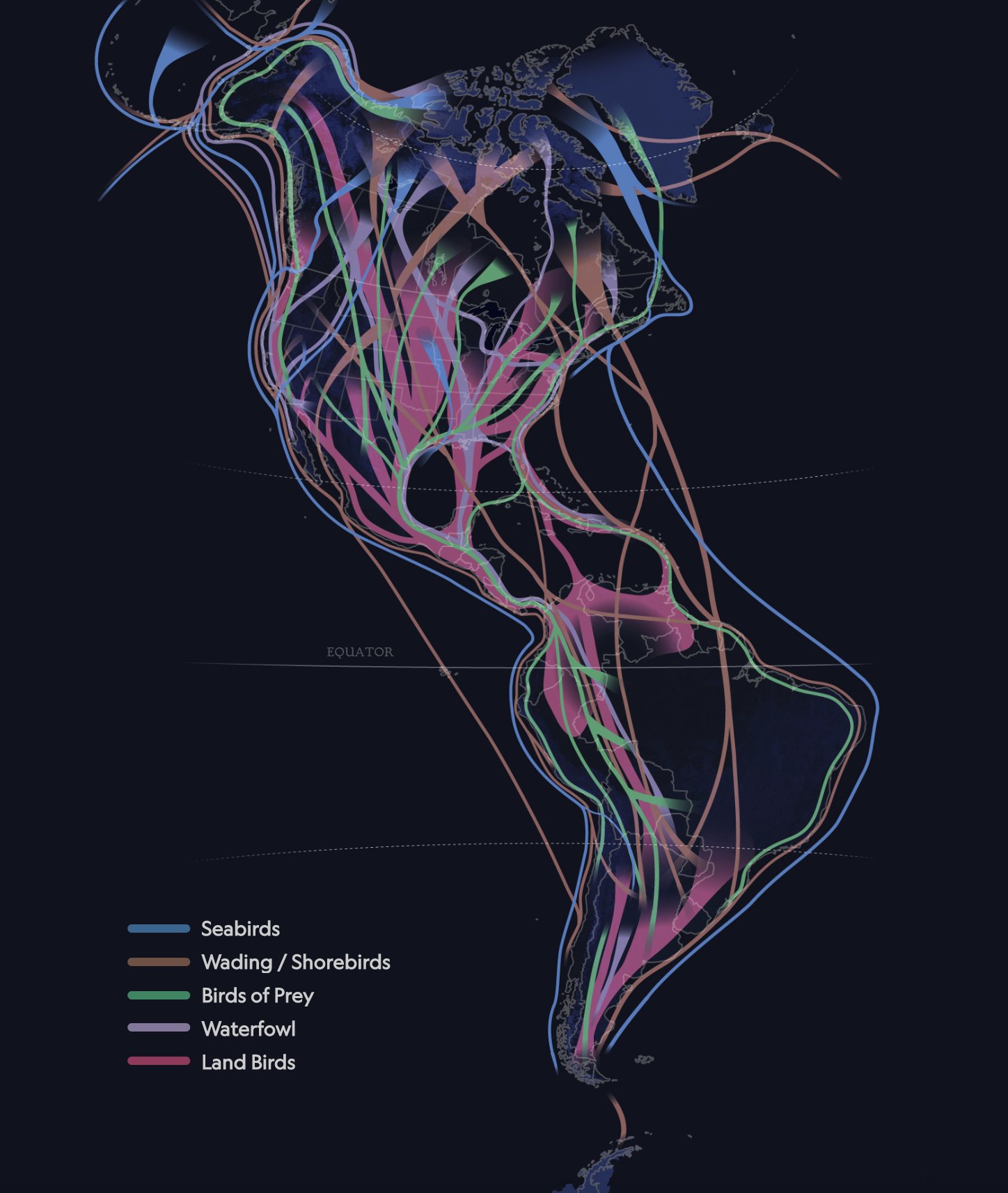
Esta visualización muestra los flujos de aves migratorias en América, donde cada flujo tiene diversas ramificaciones a partir de un camino principal. Cada tipo de ave tiene su propio set de flujos (expresado en el canal de tono). La apariencia orgánica de los flujos da a entender que las rutas pueden ser algo erráticas, que se trata de seres vivos moviéndose y adaptándose a lo que sucede en el camino. Me parece sorprendente la resistencia y fuerza de estas aves. ¿Han notado como algunas aves hacen escala en las Islas Galápagos?
Proportional Symbol Maps #
Un proportional_symbol_map es una visualización en la que sobre un mapa se posicionan glifos como marcas compuestas (ver clase de codificación visual para más detalles). De cierto modo son una extensión de un bubble_map, reemplazando la burbuja en cada posición por un glifo. De hecho, los glifos sobre los mapas tienden a ser circulares, porque esto hace más fácil su incorporación en el gráfico sin que choquen entre sí, y al mismo tiempo es más orgánico y agradable de ver. Utilizar una marca compuesta permite mostrar múltiples atributos para cada unidad de análisis. Se utiliza el nombre proportional porque el tamaño del glifo también suele expresar algún atributo. Un ejemplo típico es el siguiente, que visualiza la prevalencia de distintas enfermedades causadas por insectos en Brasil:
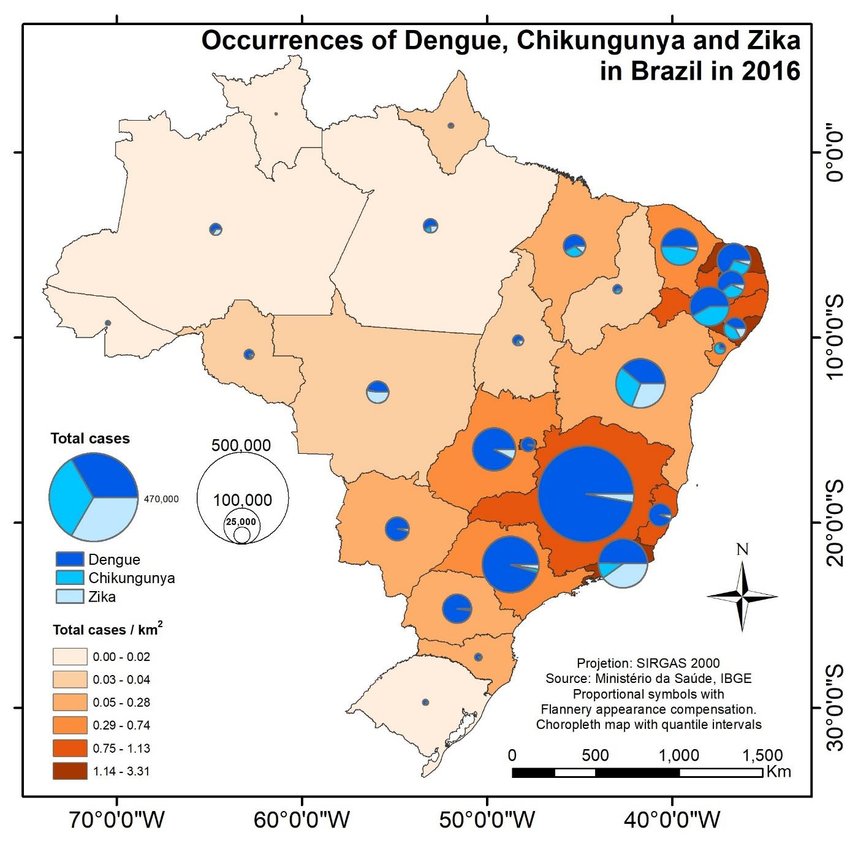
Al ver el ejemplo notamos una de las cualidades del proportional_symbol_map: se complementa bien con otro mapa que utilice una codificación visual diferente, en este caso, un choropleth_map.
Los glifos pueden ser de varios tipos. En el ejemplo anterior, un pie_chart permite mostrar la distribución interna de una variable en cada unidad de análisis. También es posible utilizar otros glifos que resuelvan tareas distintas. La siguiente visualización se llama modal_cell y presenta un glifo que codifica las direcciones y modos de transporte utilizados en cada municipalidad de Santiago:
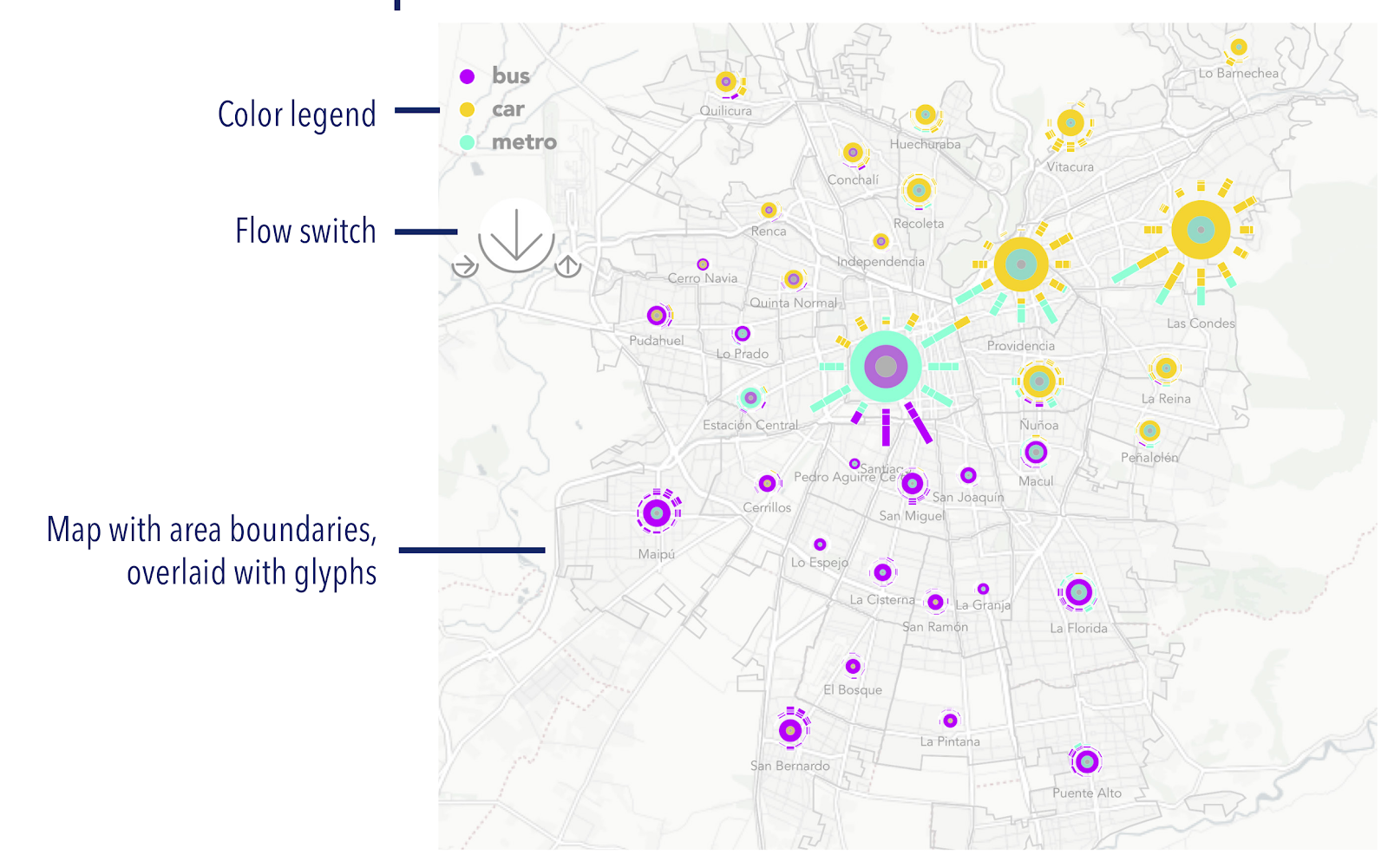
Al agregar flujos, el glifo de modal_cell permite resolver tareas geográficas: para cada comuna se puede ver cuál es el modo de transporte predominante y desde cuáles direcciones llega la gente que viaja a esa comuna para trabajar.
Flujos Vectoriales en Campos #
Tal como existen campos escalares, también existen campos vectoriales, donde para cada punto en el espacio puede haber un flujo local, una flecha que representa la principal dirección de variación o importancia de uno o más atributos. De este flujo local se puede derivar un flujo geométrico, siguiendo la trayectoria de movimiento a través de los flujos locales del campo. La visualización de este flujo geométrico permite encontrar patrones globales en el flujo. Algunos ejemplos de como luce este tipo de visualización se muestran a continuación:

Ahora bien, ¿cómo lucen estas técnicas en un mapa? Pueden ver una versión animada de la siguiente técnica en este trabajo que compara y combina técnicas de visualización de flujo:

Este tipo de visualización permite resolver tareas de búsqueda de caminos en el flujo, así como de identificación de patrones globales.
Precauciones al hacer mapas: Población y Proyección #
Quizás una de las variables que más influye en los mapas sin que nos demos cuenta es la población. Existe una tira cómica de XKCD que ilustra este concepto, donde si no tenemos cuidado podremos creer que estamos viendo una relación donde no la hay:
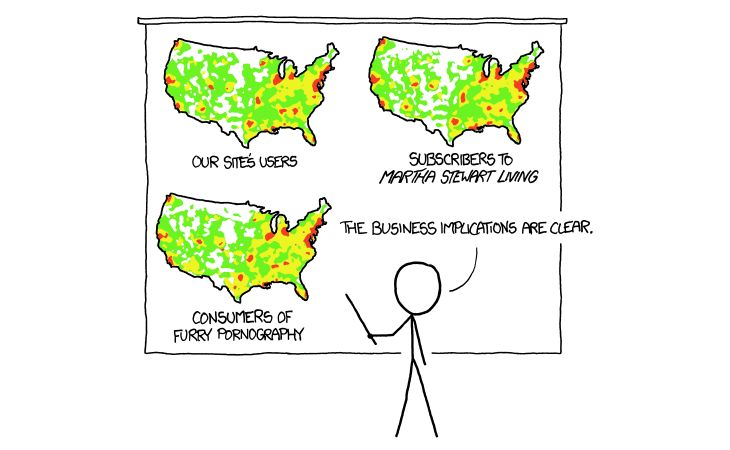
Debemos tomar precauciones para controlar el efecto de la población en nuestros datos. La medida más común es visualizar tasas o porcentajes, que no solo quitarán el efecto de la población sino que permitirán comparaciones entre las unidades de análisis.
Otro aspecto del cual quizás se dieron cuenta, es que todos los mapas que hemos presentado están en dos dimensiones. Sin embargo, la tierra no es plana. Entonces, si queremos visualizar el planeta, tenemos que “aplanarlo” para visualizarlo en 2D — eso es lo que hace una proyección cartográfica que convierte las coordenadas pseudo-esféricas de la tierra a posiciones x e y dentro de un plano 2D. Existen muchas proyecciones, algunas más conocidas que otras, y todas comparten la siguiente propiedad: se distorsiona al menos un aspecto de la geografía. ¿Por qué? Hagan el siguiente ejercicio: tomen la cáscara de una naranja e intenten aplanarla. Llegarán a la conclusión de que es imposible hacerlo sin deformarla o cortarla.
Lo mismo sucede con los mapas.
Las siguientes son algunas de las tantas proyecciones que existen:
La proyección más común es la de Mercator. Al mismo tiempo, es la peor de todas por el nivel de distorsión que genera. Éste es un tema que merece su propia clase, así que no entraremos en más detalles. Lo que sí podemos aprender es que el contexto del problema que estemos resolviendo nos ayudará a elegir una proyección. Por ejemplo, aunque Mercator sea la peor, existen sistemas de coordenadas basadas en Mercator que permiten medir las distancias en metros, y que a escalas “pequeñas” (como una ciudad) presentan una distorsión ínfima. El sistema de coordenadas para Santiago y otras partes de Chile es EPSG:5361, pero no sirve para todo el país. Hablaremos de esto en la clase práctica.
Datos Espaciales: Point Clouds #
Hasta este momento hemos ejemplificado distintas técnicas de visualización en 2D. Incluso al tener datos más allá de x e y, como la altura, podemos utilizar representaciones 2D (o 2.5D) para efectuar las tareas que necesitemos. Sin embargo, existen datos espaciales cuya naturaleza es volumétrica y que requieren visualizaciones en 3D. Este tipo de datos usualmente provienen de sensores, modelos matemáticos y cámaras especiales que captan profundidad.
Un ejemplo de dataset espacial es un conjunto de puntos con posición x, y y z. Una visualización directa de estos datos se llama point_cloud, ya que posiciona cada elemento directamente en su posición correspondiente, enfocados por una cámara con movimiento libre. El siguiente ejemplo muestra el resultado de escanear una esquina de San Francisco con el sistema LIDAR:

Aunque esta técnica muestra directamente cada punto en su posición original, no es una técnica simple de implementar. Al expresar un volumen, es posible que muchos puntos se sobrepongan entre sí dependiendo de la perspectiva de la cámara. ¿Cuáles mostrar?¿Cuáles no?¿Qué expresar con el canal de color?¿Qué tipo de cámara utilizar?¿Cómo interactuar con los puntos?
El proyecto Sonomap presenta una experiencia de realidad virtual donde una persona vuela sobre la ciudad, representada con una point_cloud, y escucha los sonidos característicos de cada lugar. De ahí su nombre de mapa sonoro de la ciudad:

En resumen, las tareas que resuelve esta visualización son explorar la distribución de los datos, y también reconocer la forma espacial de los elementos representados por puntos. Un fin de una point_cloud es servir de punto de entrada para generar volúmenes y superficies en 3D que representen entidades y objetos.
Datos Espaciales: Rendering de Volumen #
Cuando se trabaja con una point_cloud se tienen datos heterogéneos. De hecho, la imagen de ejemplo tenía puntos que pertenecían a pavimento, paredes de madera, ventanas de vidrio, postes de luz de metal, y otros elementos. Existen otros datos volumétricos donde todos los puntos, o más bien, todos los cubos o vóxeles del espacio pertenecen a un mismo contexto, como los provenientes de una resonancia magnética. En los resultados de un escáner sabemos que estamos analizando el interior de un cuerpo humano, y nuestra tarea es identificar la forma y estado de sus órganos. Así, cada celda tiene uno o más valores que contienen la lectura del escáner.
Las técnicas de volume_rendering buscan desplegar e interactuar con los elementos escaneados. Una manera de hacerlo es derivar isosuperficies de los datos, y desplegar estas superficies en la visualización. El siguiente es un ejemplo de isosuperficies derivadas del escáner de una muela:
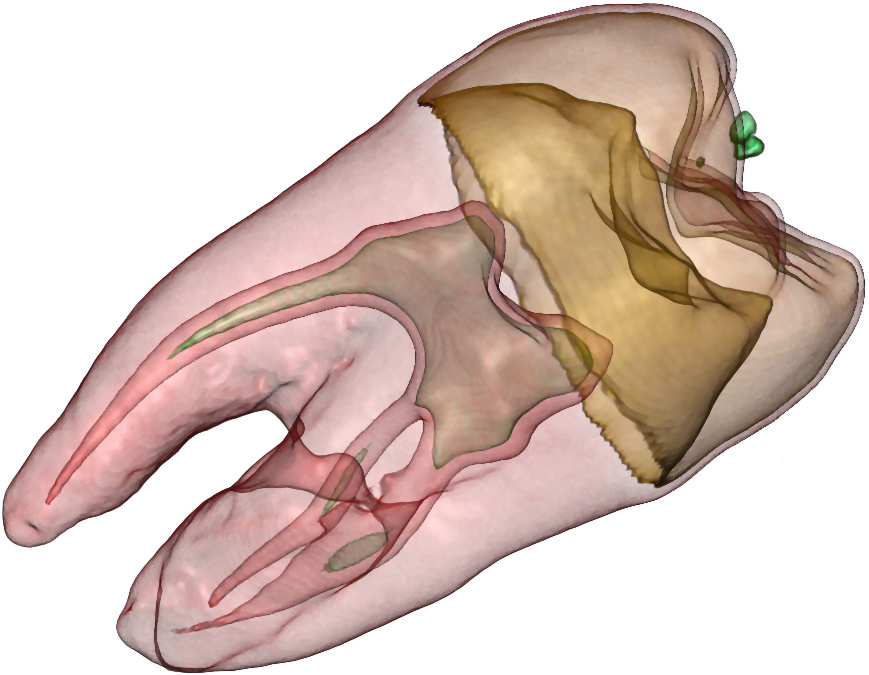
Sabemos que las distintas componentes de una muela tienen diferentes densidades, niveles de minerales, entre otras características. Un algoritmo de detección de isosuperficies utiliza esos valores para identificar la cáscara o recubrimiento (interior o exterior) para varios rangos de esos valores. Por ejemplo, detecta que el esmalte de la muela termina y comienza una cavidad nerviosa cuando la densidad baja bruscamente.
Este tipo de visualizaciones permite comprender la geometría y encontrar patrones geométricos.
Fin de Unidad: El Mapa no es el Territorio #
En esta unidad hemos explorado técnicas de visualización de datos geográficos y espaciales. De la experiencia de los cursos anteriores he aprendido que es una de las clases que tiene mejor recepción por parte de les estudiantes, quizás debido a la familiaridad de los mapas y de lo directo que es pensar en datos de este tipo. Esa cualidad hace que estas técnicas sean poderosas herramientas, ya que tienen mayor probabilidad de ser parte del marco de referencia cultural de quien diseña y de quien utiliza la visualización, facilitándonos el trabajo y aumentando las posibilidades de que nuestros resultados sean efectivos.
Sin embargo, no debemos dejarnos llevar por esta cualidad. No siempre la mejor manera de representar datos geográficos o espaciales es un mapa. Y por detallados que sean nuestros datos, debemos recordar que un mapa es siempre una abstracción. De esto nos advirtió Borges en su tiempo:
Del Rigor en la Ciencia
Jorge Luis Borges
En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él.
Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.
Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.
El mapa no es el territorio. Sí es un terreno fértil para que extraigamos valor y conocimiento de los datos utilizando visualización.
Lecturas Recomendadas #
- Andrienko, Natalia, Gennady Andrienko, and Peter Gatalsky. Exploratory spatio-temporal visualization: an analytical review. Journal of Visual Languages & Computing 14, no. 6 (2003).
- Chen, Wei, Fangzhou Guo, and Fei-Yue Wang. A survey of traffic data visualization. IEEE Transactions on Intelligent Transportation Systems 16, no. 6 (2015).