Visualización de Tablas
En esta unidad veremos técnicas de visualización para tablas, el tipo de dataset más común. Las técnicas que se utilizan con datasets de tablas suelen enfocarse en expresar el contenido de estás. Como las tablas contienen muchos elementos (o al menos podemos suponer que es así), necesitamos organizarlos (arrange) en el espacio de la visualización. Dependiendo de la tarea que debamos resolver esa organización será a través de maneras de separar las marcas, de ordenarlas, o de compararlas con una base alineada.
Además tenemos que considerar que existen distintos tipos de tablas. Si definimos que una llave (key) es la manera de identificar un elemento en una taba, podemos clasificar las tablas de acuerdo a la cantidad de llaves (keys) que tienen. Una tabla con 1 llave es una lista de elementos (que pueden tener varios atributos). Una tabla con 2 llaves es una matriz 2D. Una tabla con 3 llaves es una matriz 3D o un volumen. Y una tabla con 3+ llaves, o incluso sin un número constante de llaves, puede ser considerada como una tabla que se puede dividir recursivamente en otras tablas (recursive subdivision).
Estos conceptos son ilustrados en la siguiente imagen:
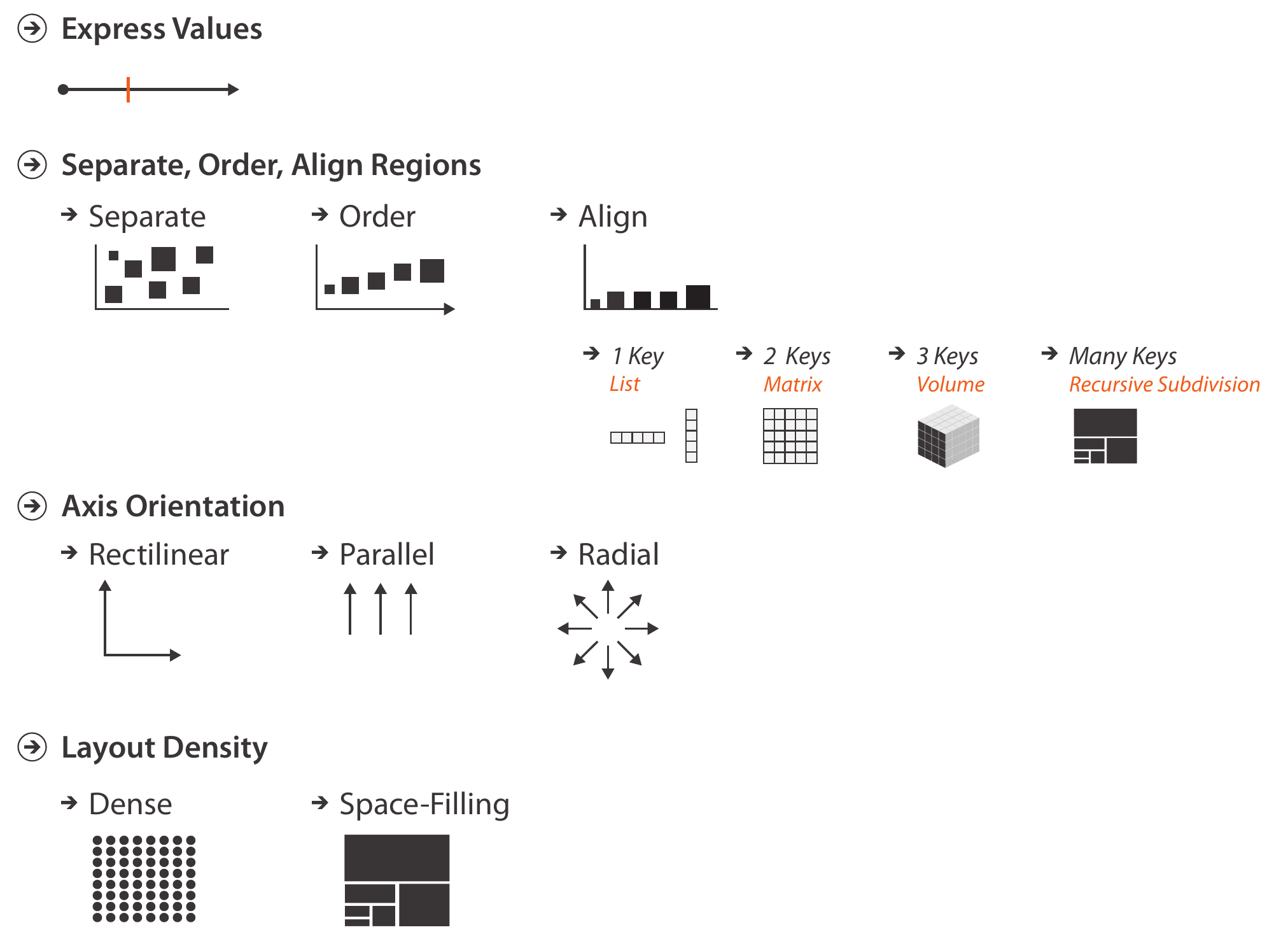
Los otros conceptos que son relevantes a la hora de organizar elementos son la orientación de los ejes y la densidad de a organización. Tradicionalmente la orientación es rectilínea y ortogonal (como en los típicos ejes x e y), pero también puede haber ejes paralelos y radiales. Respecto a la densidad, hay dos tipos: densa, en la que puede haber muchos elementos en pantalla, pero también hay espacio que no es utilizado, o exhaustiva (space-filling), porque utiliza todo el espacio disponible (es decir, cada píxel) independiente del número de elementos.
En esta unidad comentaremos técnicas de visualización para resolver tareas con tablas. Comentaremos estos aspectos de las visualizaciones, y también responderemos preguntas relevantes, como ¿para qué tarea se utiliza esta visualización?¿cuál codificación visual utiliza?¿cuántos datos puedo mostrar sin sacrificar eficiencia?
Iniciemos el recorrido.
Scatterplot / Gráfico de Dispersión #
El clásico scatterplot es un gráfico denso que expresa atributos cuantitativos. Se suele ver así:
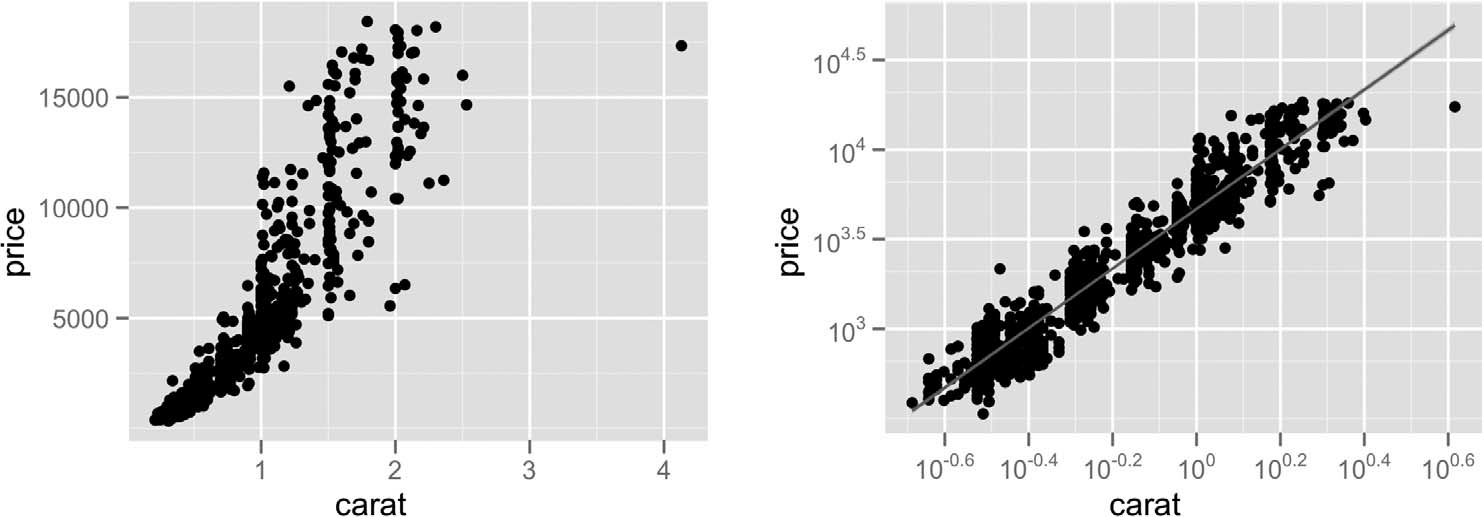
Como datos, el scatterplot utiliza 2 atributos cuantitativos de la tabla. No usa las llaves de ésta en tanto no le importa el identificador de cada elemento (pero sí los nombres de los atributos). La marca utilizada es un punto por cada observación), que es posicionada en el espacio a través de los canales de posición en x e y.
Este gráfico se utiliza para encontrar patrones, outliers, distribuciones, correlaciones, e identificar clústers. Su escalabilidad es limitada, podemos mostrar cientos de observaciones. Con más la puede haber demasiada sobreposicioń (overlapping), de modo que por mostrar mucho no vemos nada.
El siguiente es un scatterplot que grafica ejemplifica algunas tareas:
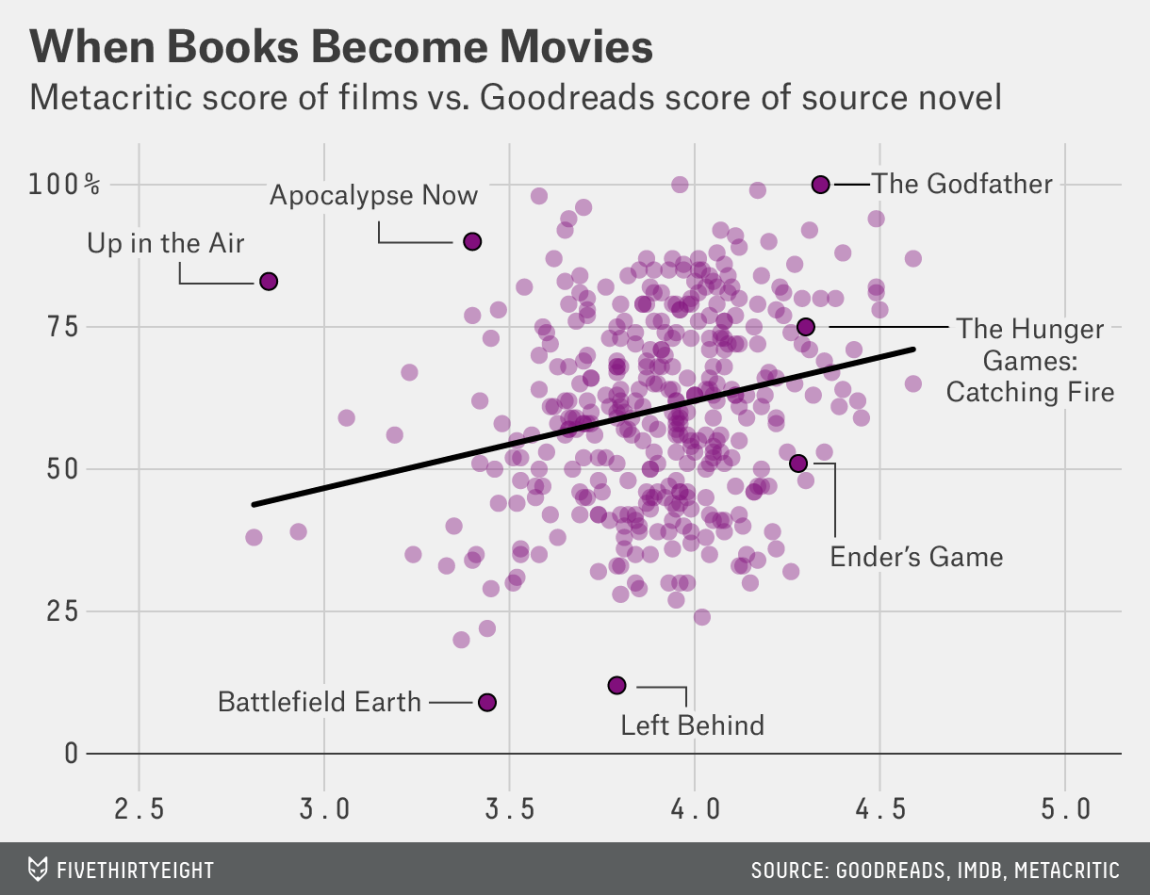
Esta visualización nos muestra la correlación entre la crítica de un libro (eje x) y la crítica de la película que adapta cada libro (eje y). Al mismo tiempo, se encarga de anunciarnos los outliers, que son de varios tipos, como aquellos libros malos con películas horrendas (Battlefield Earth), y aquellos libros buenos con películas aclamadas (The Godfather).
El scatterplot es parte de la navaja suiza de toda persona que haga visualización. Es un buen punto de partida para explorar un dataset.
Line Chart / Gráfico de Líneas #
El linechart es otro gráfico clásico. Al igual que el gráfico anterior, muestra dos valores cuantitativos; a diferencia, uno de éstos valores es la llave de la tabla. La marca son puntos conectados a través de líneas, lo que configura una polílinea en la visualización (los puntos pueden tener tamaño 0, de modo que solamente la línea es visible). Este ejemplo nos muestra el peso de un gato (atributo) a lo largo de los años (llave):
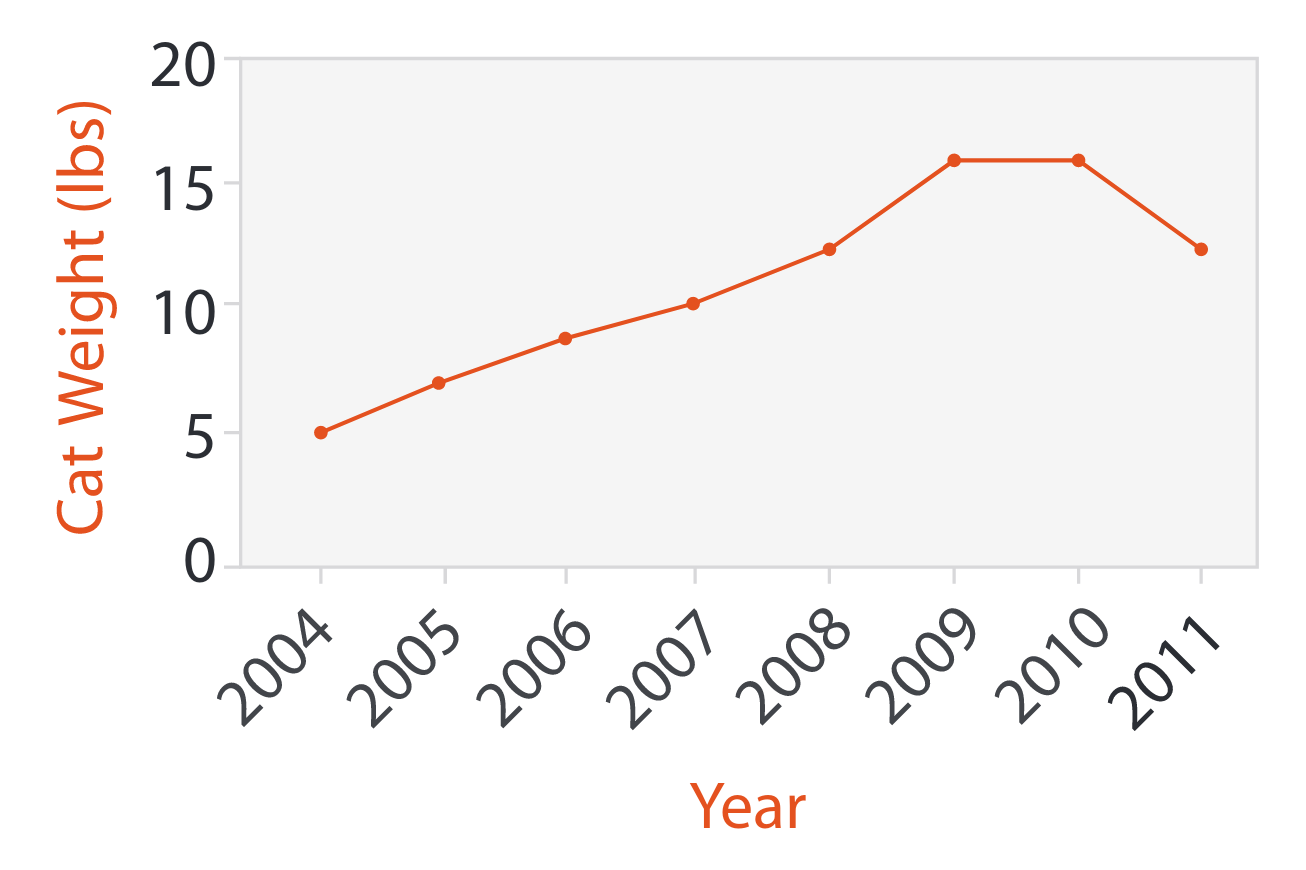
Nos damos cuenta que la posición vertical de los puntos expresa un valor cuantitativo, y la posición horizontal es ordenada por la llave. El orden de la llave es importante: este gráfico no tendría sentido si los años estuviesen dispuestos al azar, porque las líneas que conectan cada par consecutivo de puntos enfatizan la relación que hay entre un ítem y el siguiente.
El orden es el que permite que en un linechart se pueden realizar tareas de encontrar tendencias y patrones. También resulta directo encontrar extremos locales y globales.
El ejemplo del linechart nos permite ejemplificar el uso de las llaves. La llave en el ejemplo es el tiempo porque es el atributo que identifica a cada observación — un año no se puede repetir en esos datos, pero un peso sí.
Ahora bien, ¿qué pasa si tenemos múltiples entidades en un gráfico? Veamos un linechart con múltiples líneas:
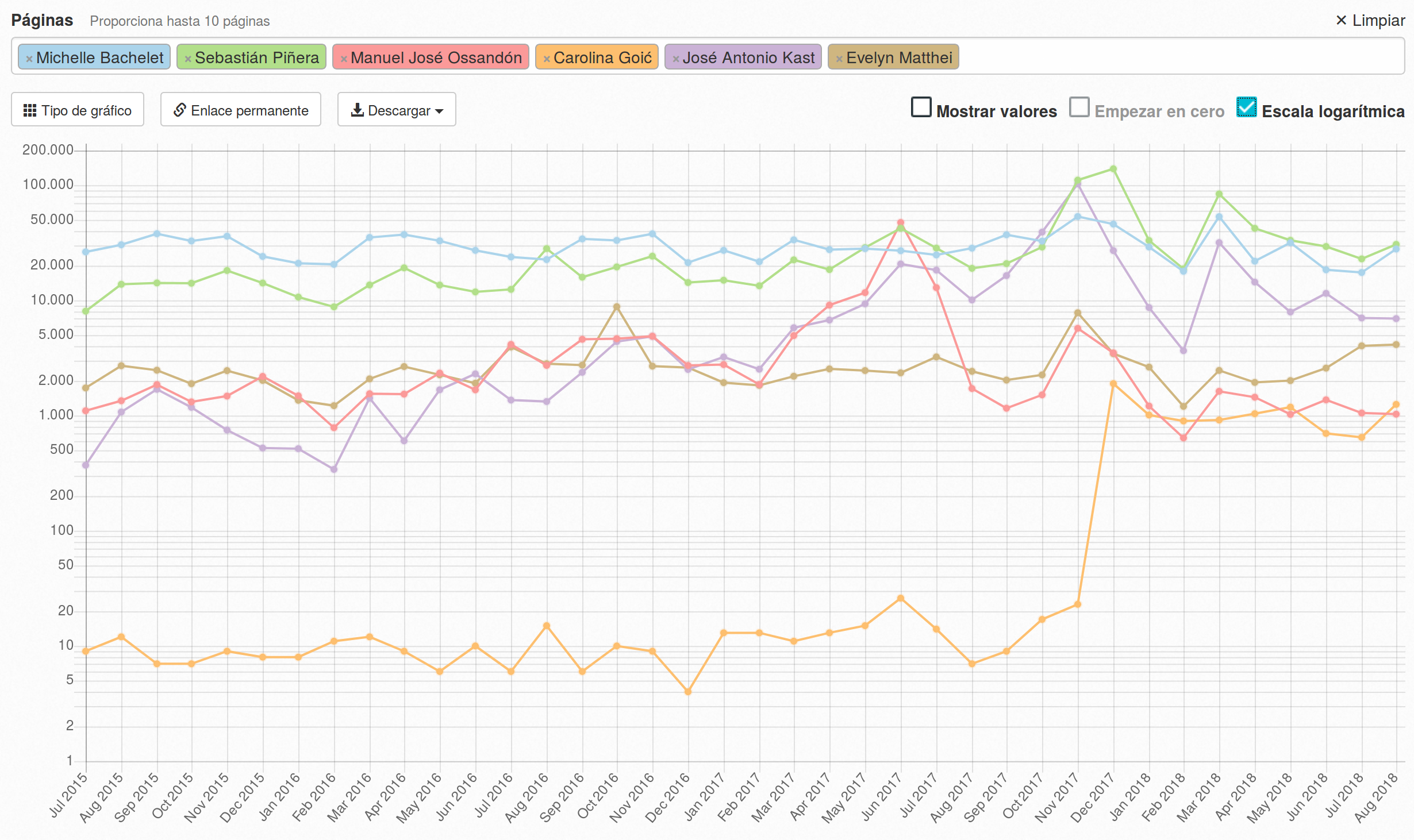
Este gráfico creado en una herramienta de Wikipedia nos muestra la cantidad de visitas que recibieron los artículos de les candidates presidenciales de la última elección en Chile. Este gráfico tiene dos llaves, de modo que podemos identificar el número de visitas (atributo) en una fecha determinada (llave 1) a un artículo (llave 2).
Otra característica del ejemplo es que su canal de posición para el atributo cuantitativo utiliza una escala logarítmica en vez de una escala lineal. Eso permite comparar tendencias en el orden de magnitud de la serie temporal más que en la magnitud en sí misma. Prueben en la herramienta como luce el gráfico con la escala tradicional — notarán que los insights que se obtienen del gráfico son otros. Por ejemplo, en este gráfico se aprecia cuándo Carolina Goic se anunció como candidata gracias a la escala logarítmica. En la escala lineal, debido a la magnitud que tienen otras personas más populares, los cambios en esa tendencia se pierden.
Bar Chart / Gráfico de Barras #
Para cerrar la trilogía de clásicos estudiaremos el barchart. Esta visualización expresa un atributo categórico y uno cuantitativo de la siguiente manera:
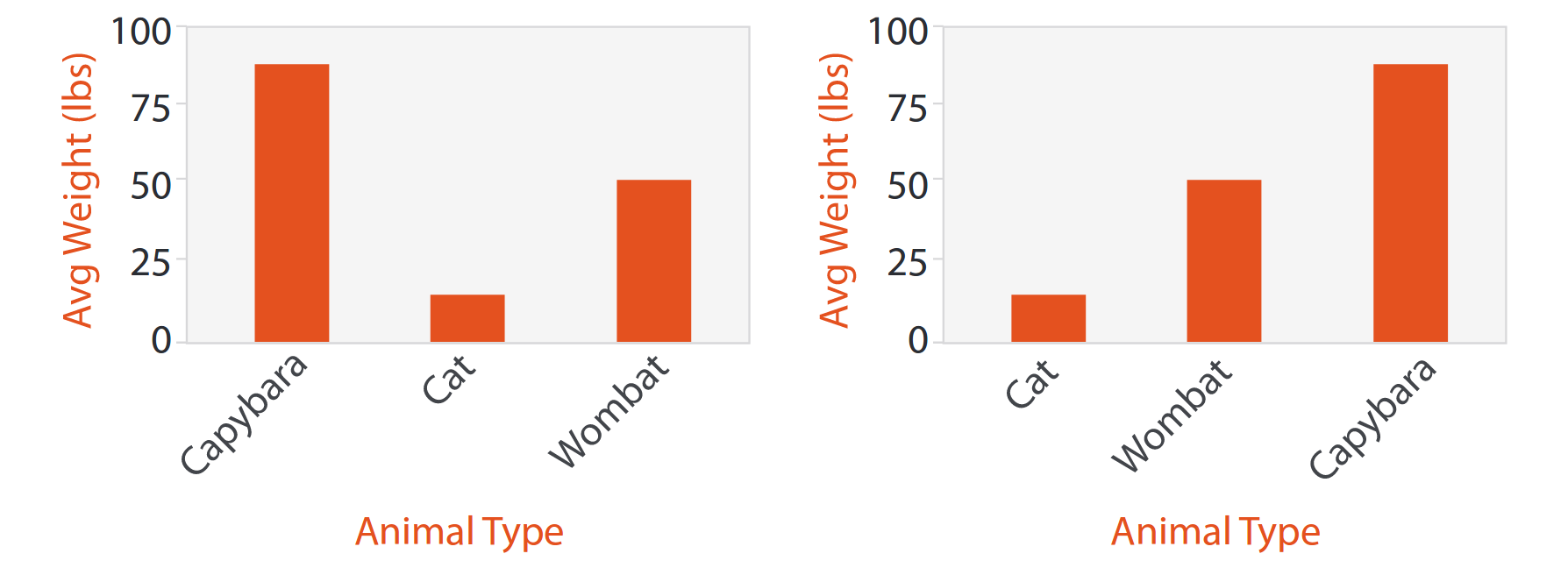
El ejemplo muestra dos gráficos para enfatizar que tenemos un atributo categórico (la raza de un animal) y un atributo cuantitativo (su peso promedio). La marca es una línea, que consideramos una barra debido a su grosor. El canal de largo de la barra nos permite expresar el valor cuantitativo, y la ubicación de la barra en cada región del espacio (definiendo una por marca o barra) nos permite expresar el valor categórico. Hay dos ejemplos para ilustrar que aquí sí tiene sentido establecer distintos órdenes para el atributo categórico: a la izquierda se ve el orden alfabético; a la derecha, el orden de acuerdo al valor, de menor a mayor.
Las tareas que permite un barchart son comparar, encontrar valores, encontrar extremos. Se pueden mostrar de decentas a cientos de niveles para el atributo llave, pero no más, de otro modo se vuelve difícil distinguir barras y sus etiquetas.
Ilustremos un uso con más categorías y con una configuración de canales distinta. Este gráfico muestra el uso de transporte público en comparación al privado en cada comuna de Santiago:
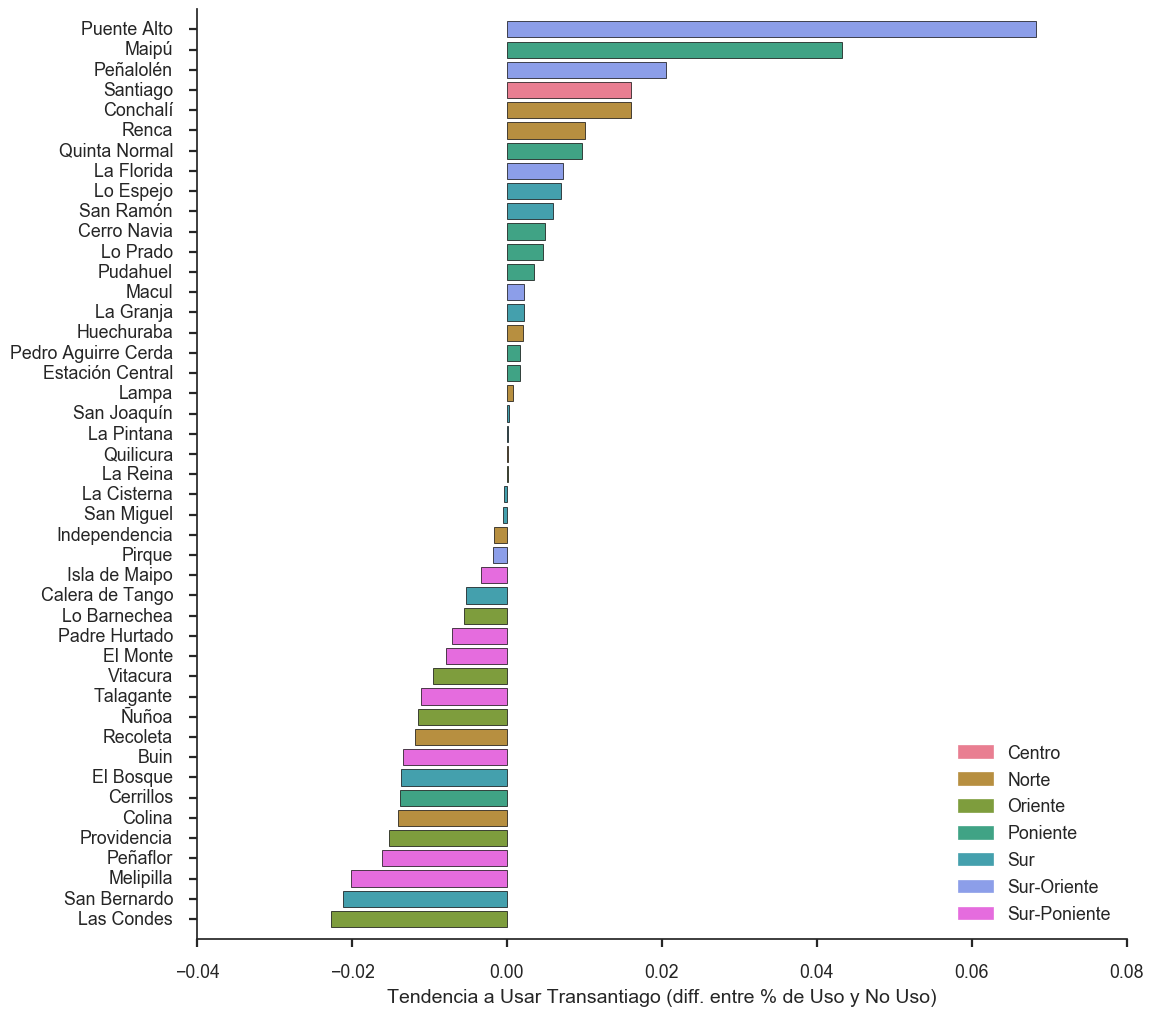
Lo primero que vemos es que los canales para la llave y el atributo cuantitativo han cambiado de rol — ahora las barras son horizontales. También apreciamos que el valor que expresan las barras puede ser divergente, lo que causa que un grupo de barras apunte en una dirección y otro grupo en la dirección opuesta. Además se utiliza un canal adicional, el tono de cada marca, para expresar otro atributo categórico (el sector al que pertenece cada comuna).
Un barchart es un gráfico que, pese a la rigidez que parezca comunicar un grupo de barras alineadas, es en realidad flexible para realizar múltiples tareas, de apariencia configurable, y fácil de componer con otras visualizaciones para crear visualizaciones profundas, atractivas y sobretodo, eficientes.
¿Cuándo usar barras o líneas? #
Tanto linechart como barchart visualizan dos atributos, y es posible hacer que el atributo categórico del barchart funcione como llave en el linechart Sin embargo, que sea posible lo significa que sea correcto. Veamos dos ejemplos donde se visualiza la altura de dos grupos de población, primero por sexo y luego por edad:
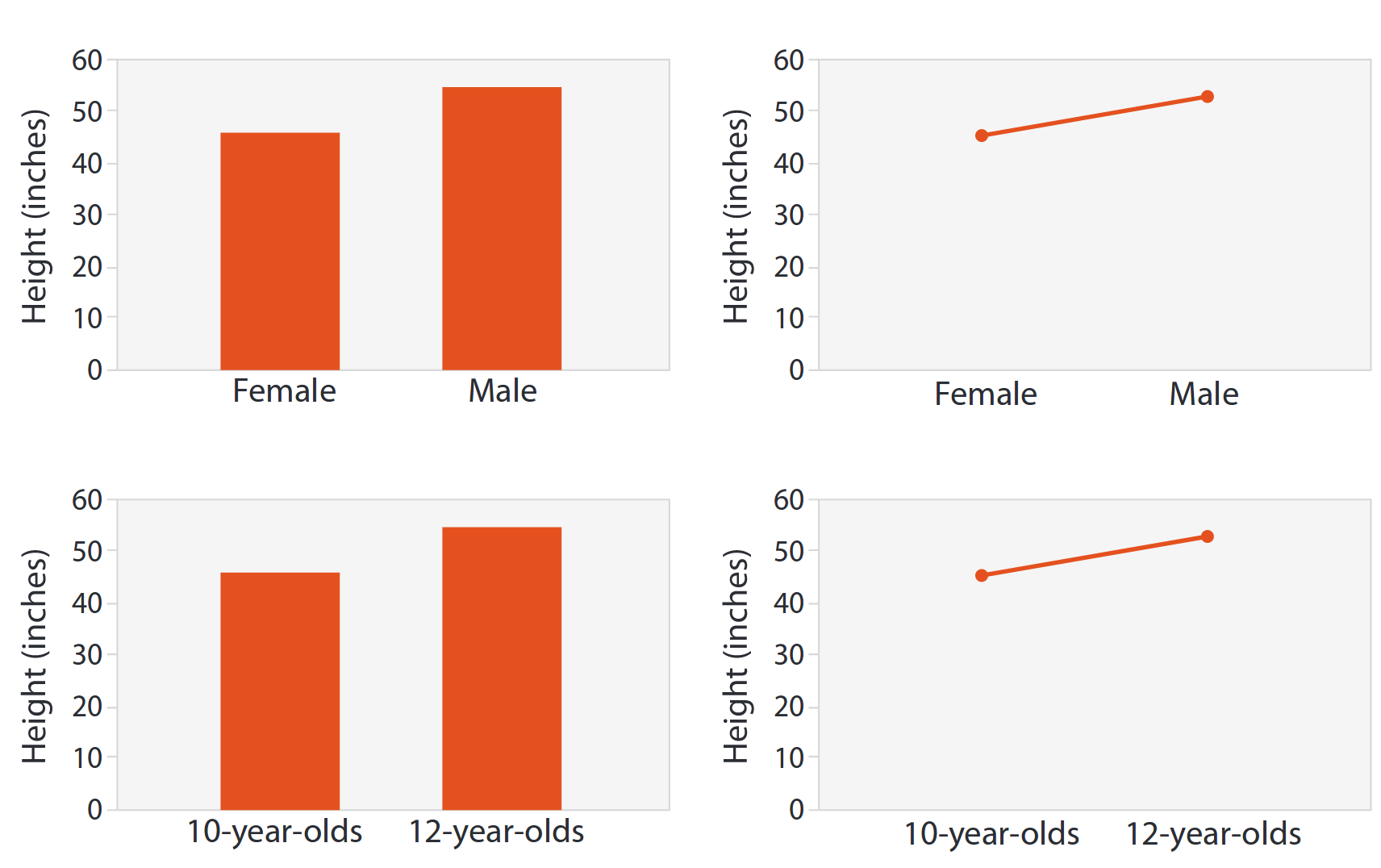
La fila superior muestra como variable categórica el sexo (binario, hombre o mujer) y la fila inferior muestra una variable cuantitativa (10 o 12 años). Nos damos cuenta que un gráfico de barras se puede usar siempre (lo que no significa que siempre sea óptimo usarlo), en cambio, el gráfico de líneas para la variable sexo no es adecuado, ya que puede llevar a un error de interpretación. En el caso de la edad, una persona podría mirar el punto medio de la línea, e interpolar los valores de modo de calcular una aproximación de la altura para los 11 años de edad. Realizar el mismo proceso para la variable sexo es errado, puesto que es un valor categórico no ordinal.
¿Cuál usar? En resumen, barchart si la llave es categórica, linechart si es ordinal o cuantitativo. Usar linechart con llaves categóricas no ordinales rompe el principio de expresividad.
Stacked Bar Chart #
El stacked_barchart es un gráfico de barras apiladas. Esto quiere decir que ya no usamos solamente una barra por categoría, sino múltiples, una sobre otra. Como ejemplo, el siguiente gráfico demuestra como distintas componentes de un sistema computacional (procesador, procedimiento, estructura de datos) intentan leer información que no están en la memoria caché, forzando una lectura lenta del sistema para traer datos a la memoria. Ese tipo de análisis es crucial es la implementación de aplicaciones y sistemas de alta performance:
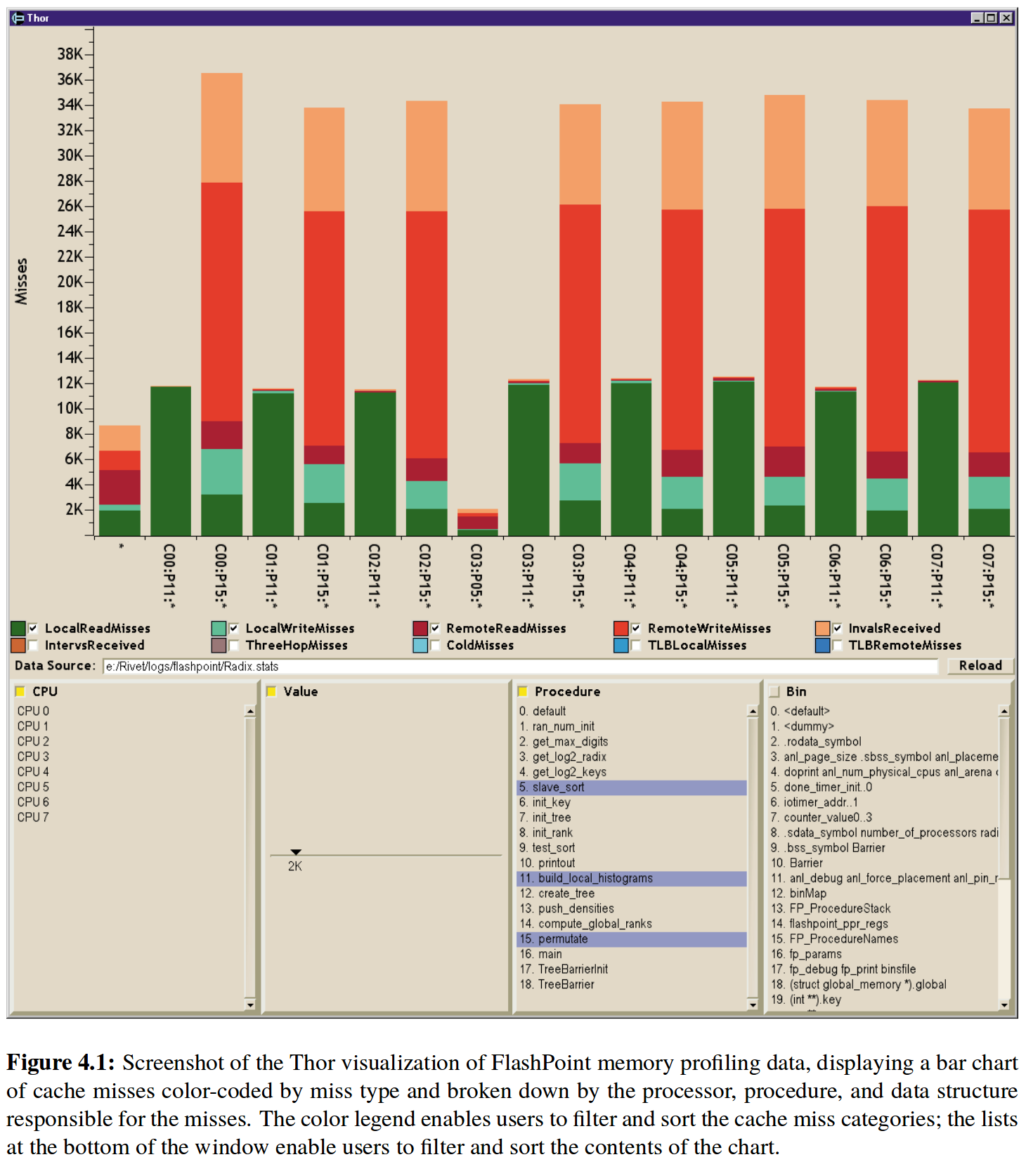
Para generar este gráfico necesitamos un atributo extra, otro atributo categórico (sumado al categórico y al cuantitativo que ya teníamos). La marca es una pila vertical de múltiples barras, un glifo que compone múltiples marcas. Los canales son el largo de cada barra, la región espacial (una por glifo, expresando a la categoría principal), y el tono de cada barra (expresando a la categoría secundaria dentro de cada glifo).
Al ser un barchart anidado, el stacked_barchart hereda las operaciones del gráfico base, añadiendo la tarea adicional de ver relaciones de parte con el todo. Su escalabilidad para el atributo categórico principal sigue intacta, pero respecto al atributo utilizado en la pila, no es recomendable ir más allá de una docena de niveles.
Noten que los glifos se alinean a través de la barra que está en la posición inferior. Por tanto, las operaciones de comparación serán más fáciles con esas barras que con el resto.
Normalized Stacked Bar Chart #
Existe una variación para el gráfico anterior, llamada normalized_stacked_barchart. Como lo dice su nombre, este gráfico normaliza cada glifo — es decir, antes de graficar cada glifo, divide los valores de cada barra por la suma total de valores en el glifo. De este modo, todos los glifos tienen el mismo tamaño y utilizan todo el espacio vertical. El siguiente gráfico con la distribución de uso de modo de transporte en Santiago ejemplifica esto:
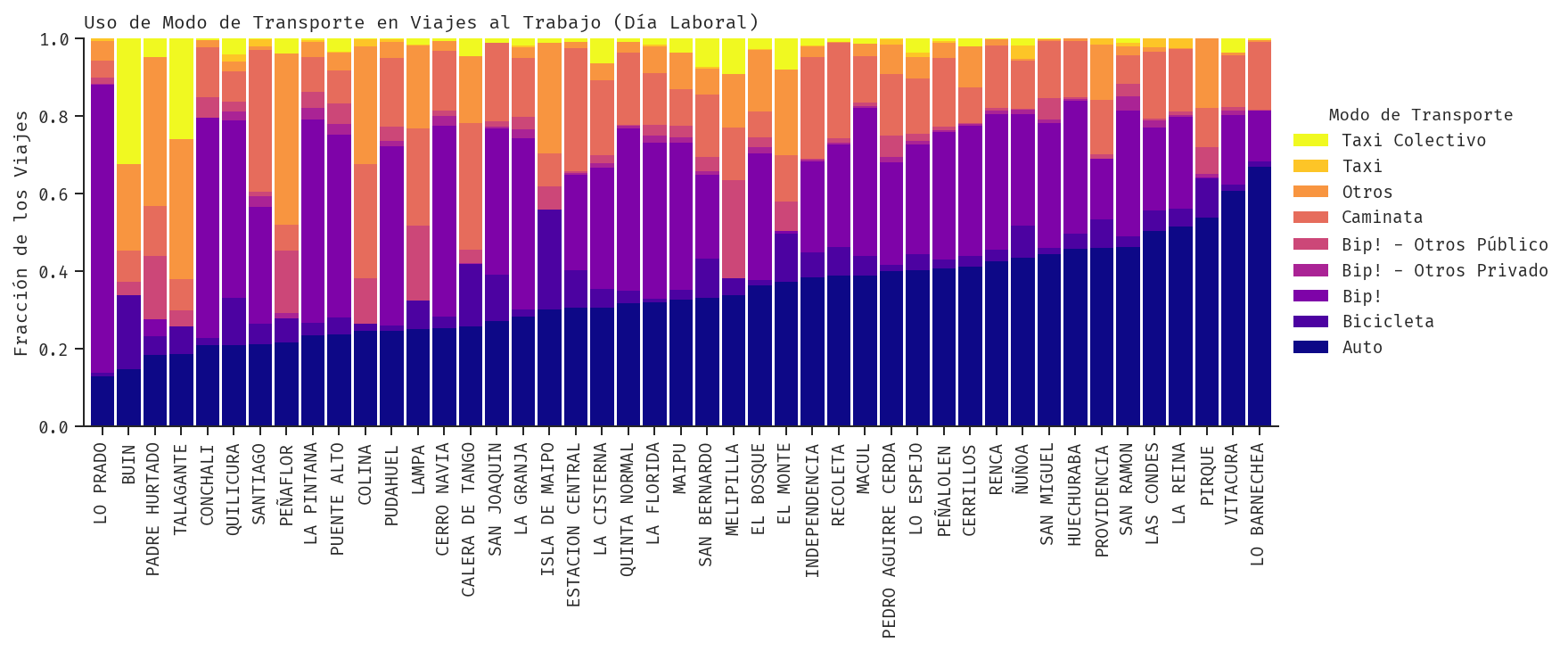
Sabemos que cada comuna tiene una población distinta, por tanto, en un gráfico sin normalización veríamos el total de viajes por modo de transporte en cada comuna. Eso puede ser informativo, pero si nos interesa un valor relativo que nos permita comparar proporciones, el gráfico normalizado nos permite hacerlo, facilitando las tareas de entender relaciones parte-de-un-todo, y comparaciones relativas.
Marimekko Chart (o Mosaic Plot) #
¿Qué sucede cuando al normalized_stacked_barchart le agregamos un canal para otro atributo cuantitativo? En la siguiente imagen se despliega como cada estado (atributo categórico) en los Estados Unidos generó energía eléctrica. El glifo codifica la distribución de las fuentes de energía (atributos categórico secundario para el color, y el atributo cuantitativo para el tamaño). La cantidad de energía total generada por cada estado es expresada en el canal de grosor de cada glifo:
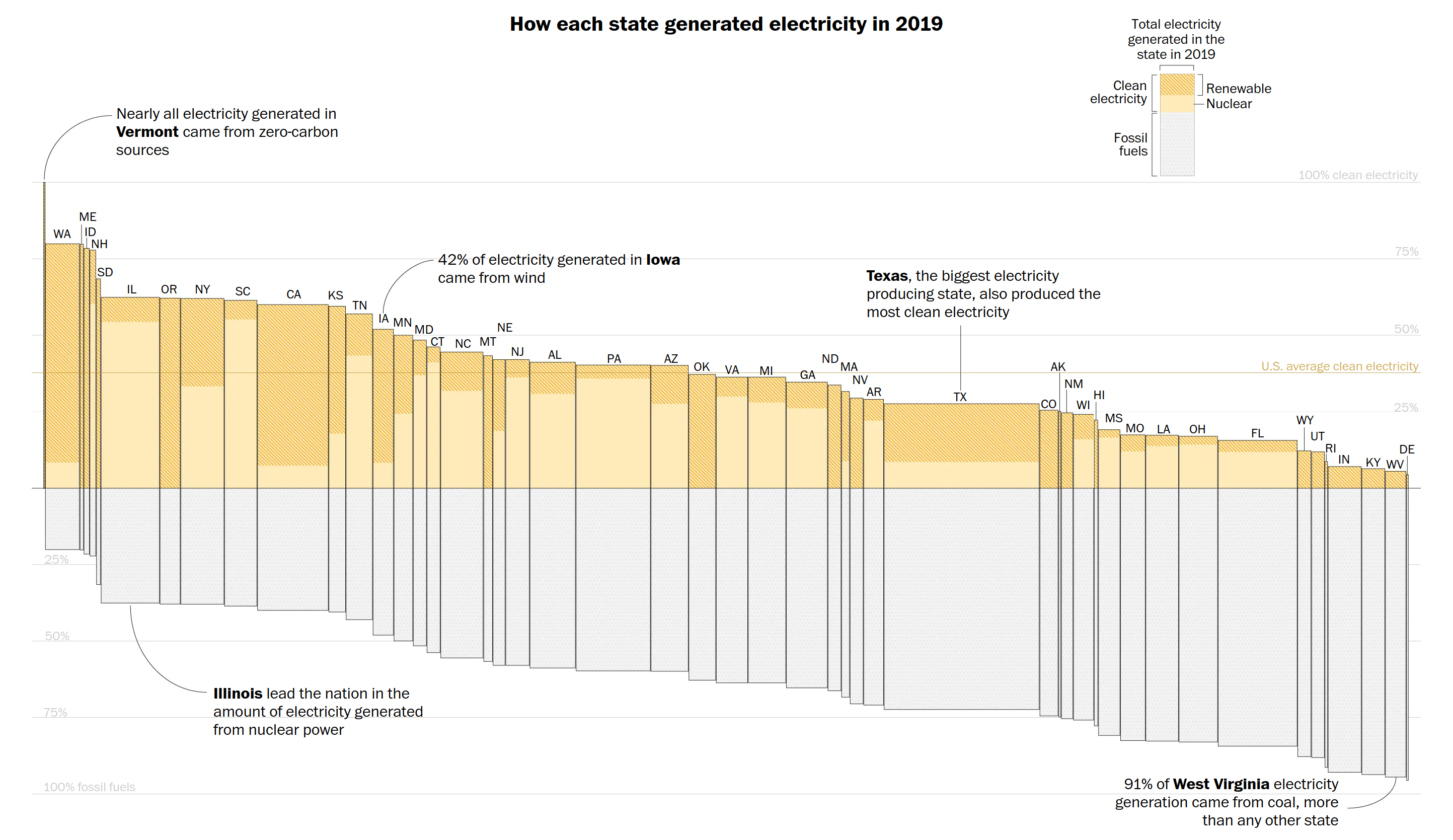
El Washington Post publicó esto. Además, quienes diseñaron el gráfico tomaron decisiones de diseño brillantes: la paleta de colores que utilizó para cada fuente de energía tiene relación con su tipo (limpia o no), y el alineamiento de los glifos sutilmente divide las energías limpias de las sucias. Con esto enfatizan ciertas interpretaciones por parte de quien lee y observa la visualización.
Este tipo de visualización es conocida como marimekko_chart o mosaic_plot.
Stacked Area Charts y Streamgraphs #
Del mismo modo que un linechart presenta una llave de tipo cuantitativa u ordinal, y el barchart de tipo categórica, el stacked_area_chart presenta una llave de tipo cuantitativa u ordinal. Así, pasamos de una o más línea que expresaban valores, a una o múltiples áreas que expresan valores: la visualización presenta distintas capas (layers). Esto implica que necesitamos un atributo adicional que se codifica en un canal: el orden de estas capas. El sitio Storytelling with Data nos brinda un ejemplo que visualiza la venta de música en distintos formatos:
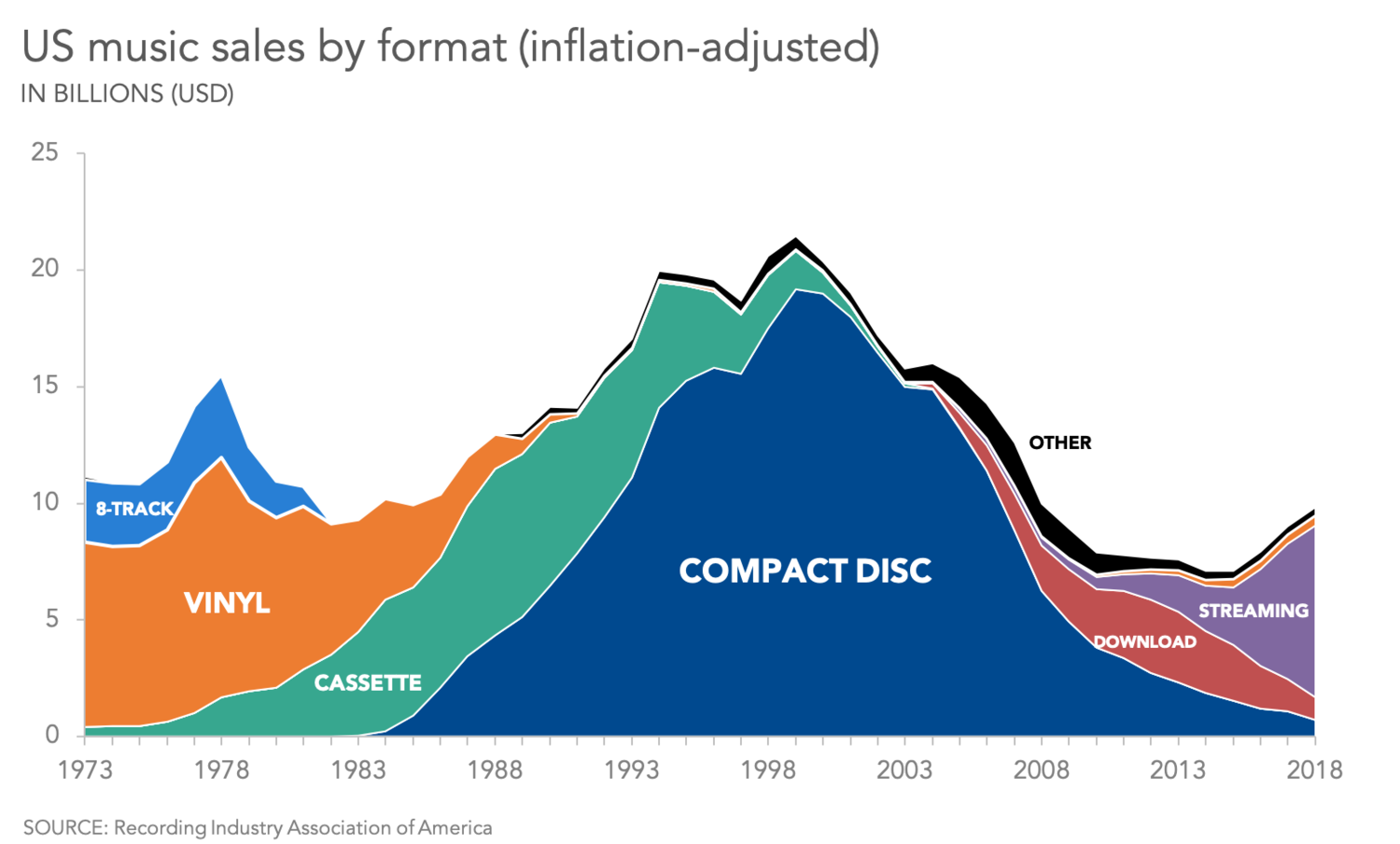
Para cada año existe un volumen de ventas de cada medio. Se aprencia claramente la edad dorada de las cintas y los CDs, y la emergencia del streaming. ¿Alcanzaste a comprar cassettes de música? Creo que el primero que me regalaron fue Use your illusion II de Guns ’n Roses.
La siguiente imagen ilustra que un stacked_area_chart puede usar distintas funciones de conexión entre elementos de la llave índice (años en este caso). Por ejemplo, se puede usar la _step function_o función escalonada que hace que tenga una curva que no es suave, pero que no fuerza interpolaciones entre observaciones, dando a entender que hay una medición por año. La visualización se refiere a la carrera por llegar al espacio:
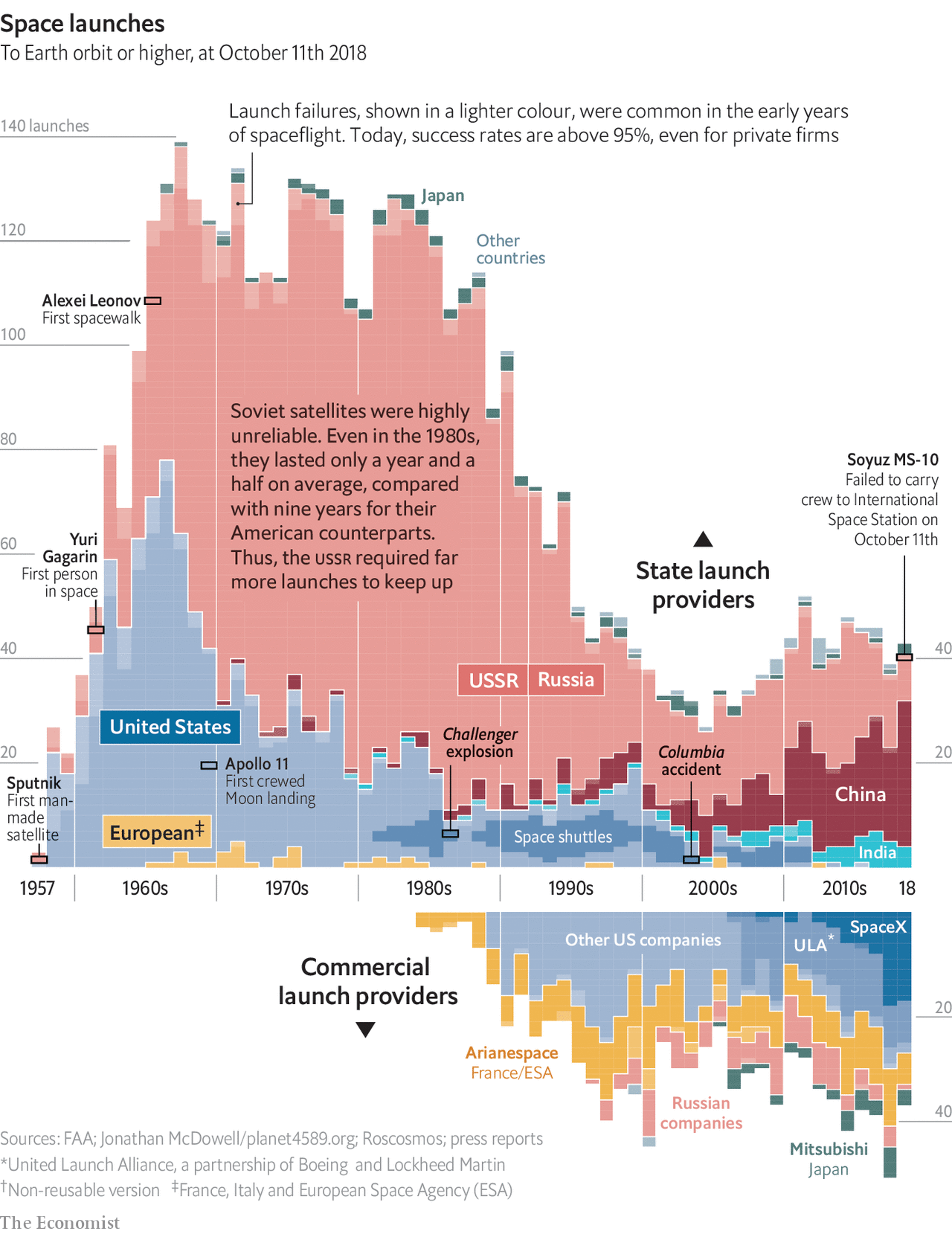
Como vemos, el atributo categórico de cada año es un país, y el valor es la cantidad de lanzamientos al espacio al año. El gráfico tiene una curiosidad y es que en realidad son dos visualizaciones: una superior, ya descrita, y una inferior, donde el atributo categórico es una compañía privada. La codificación visual es similar, pero el canal de largo de los glifos está invertido. Así, tenemos una separación clara entre entidades (países / privados).
Esa separación nos lleva a mostrar un tipo de visualización derivada, conocida como streamgraph. Los streamgraph generalizan las visualizaciones de áreas apiladas al definir una base que no es constante para los glifos — hasta este momento, todos los glifos han estado alineados respecto a un eje. ¿Qué pasa si ese eje es variable?
Así se ve un streamgraph de acuerdo al paper que estableció su definición formal:
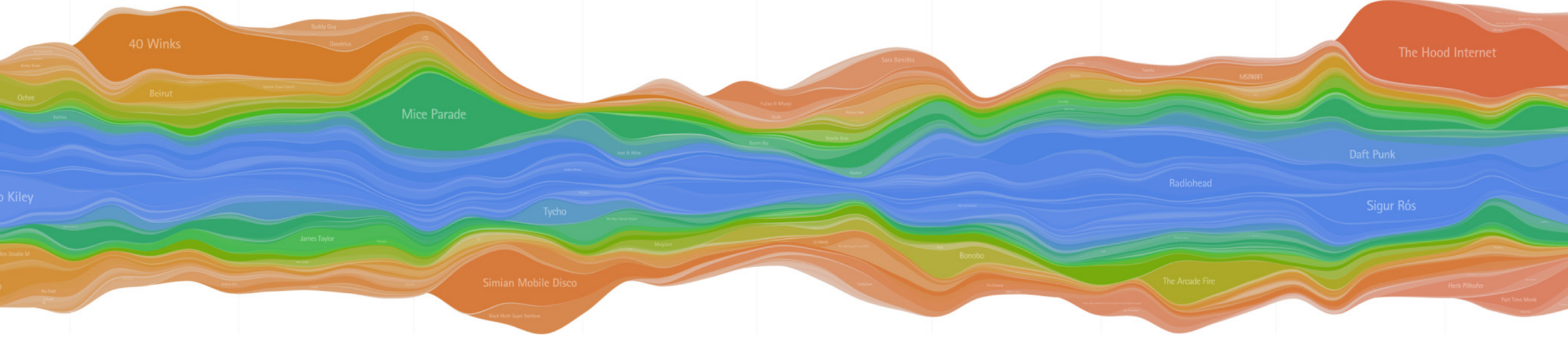
Esta visualización tiene una apariencia orgánica que puede ser atractiva si se configura bien. Mencioné que el paper la define formalmente porque antes ya existían técnicas similares, pero la definición de streamgraph las generaliza. Por ejemplo, el stacked_area_chart es un caso especial de streamgraph donde la base es una recta.
En tiempos de COVID-19 también se han realizado visualizaciones que incluyen streamgraph (y normalized_stacked_bar_chart), como muestra este artículo del Financial Times:
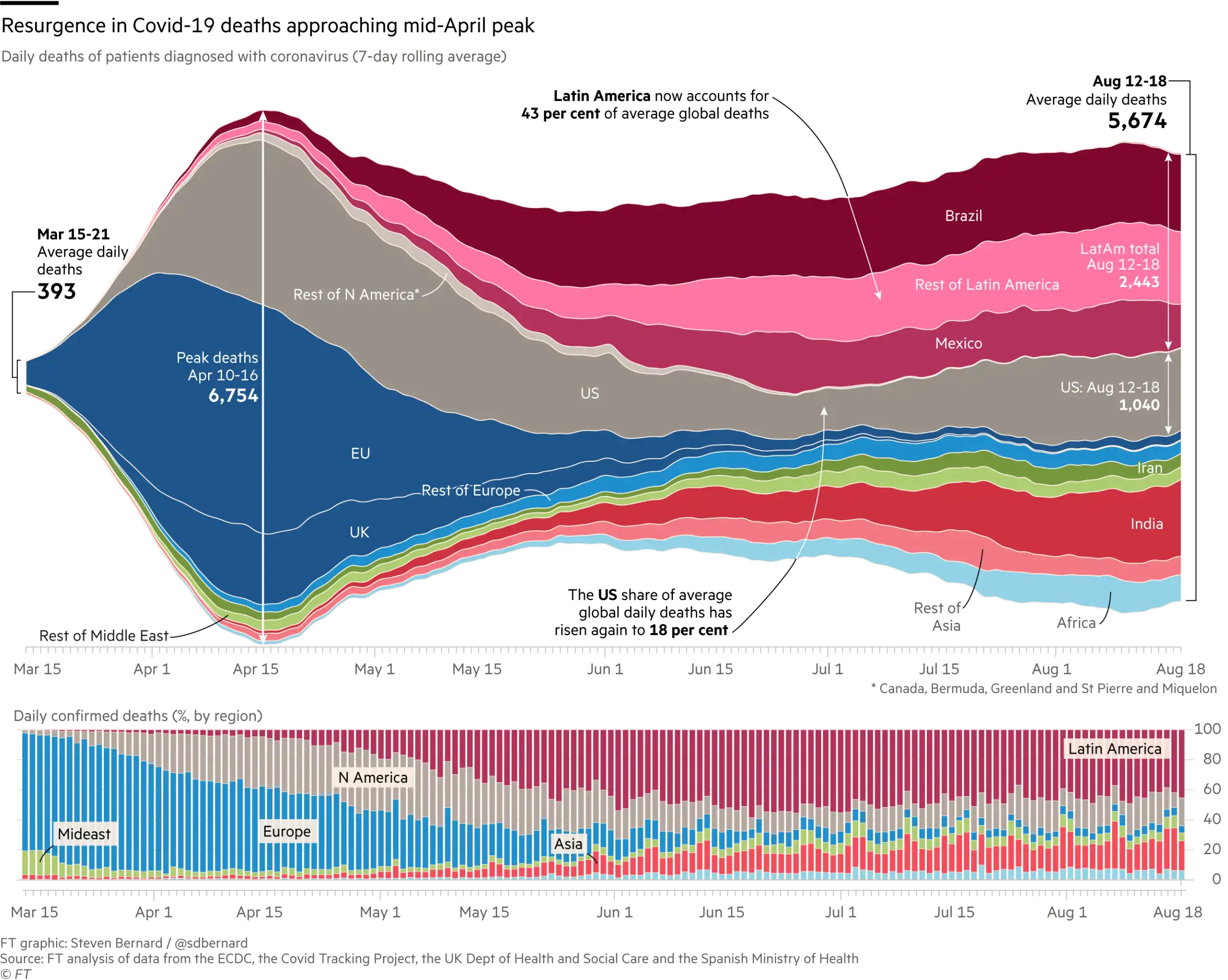
Pongamos la atención en el streamgraph: el no tener una base fija nos facilita la comparación entre el número de muertes relacionadas a COVID-19 entre cada país/región. El tono de las áreas, así como el orden de las capas, nos permite realizar las tareas que hemos comentado anteriormente no solo para áreas específicas sino también para gruposde éstas.
Aunque esta última visualización tenga pocas áreas (en orden de decenas), un streamgraph puede mostrar hasta cientos de llaves temporales debido a la amplitud de la ventana temporal que puede desplegar. En comparación, el stacked_area_chart no tiene la capacidad de mostrar tantas. El motivo, más que en las técnicas de visualización, está en los datos: en un streamgraph se suelen mostrar períodos de tiempo con áreas que destacan mucho en un solo instante, dejando espacio libre en otros momentos, mientras que en un stacked_area_chart la variación no es tanta.
Normalized Stacked Area #
Éste gráfico es el análogo del normalized_stacked_barchart, pero para áreas. Quizás uno de los gráficos de tipo normalized_stacked_area que más me ha inspirado es el siguiente, proveniente del New York Times (aunque ya no funciona en todos los navegadores debido a la tecnología que utilizaba), mostrando las rutinas diarias de las personas en Estados Unidos de acuerdo a una encuesta de uso del tiempo:
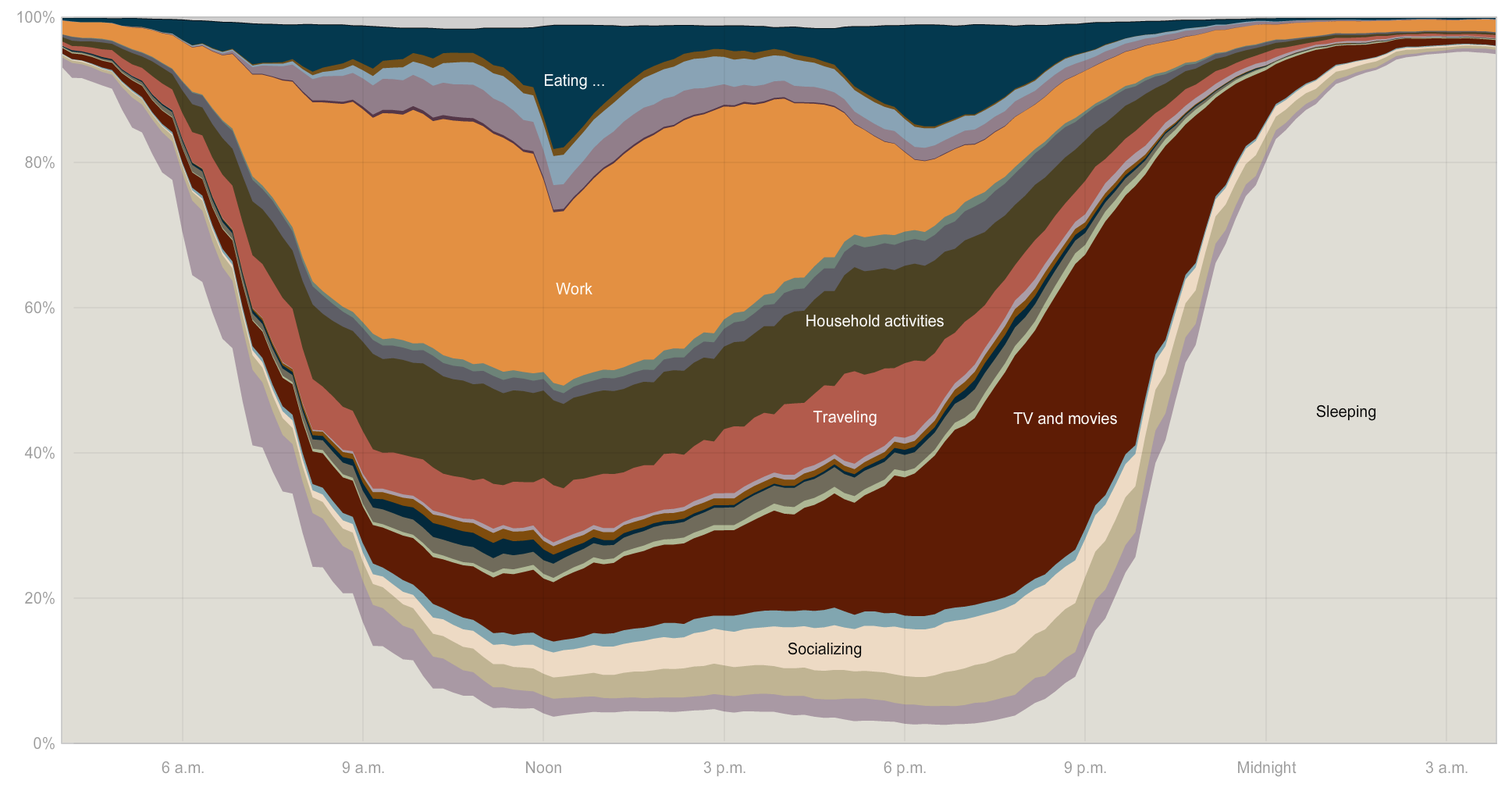
La rutina desplegada en la imagen representa el promedio de la población. Sin embargo, la visualización no se limita a eso — mediante controles de interactividad, era posible ver el mismo gráfico para hombres, mujeres, personas sin empleo, ancianes, gente de color, etc. La interactividad resaltaba las diferencias e injusticias de la sociedad, al mostrar que no todo el mundo dedicaba el mismo tiempo a las actividades de ocio, sociabilidad, relajo e incluso al descanso.
Heatmap / Mapa de Calor #
Las visualizaciones anteriores eran de tipo denso, utilizaban ejes rectilíneos, y trabajaban con datos de una llave. En cambio, la visualización heatmap es de tipo space-filling y trabaja con datos de dos llaves, es decir, con matrices. El siguiente es un ejemplo de un heatmap básico:
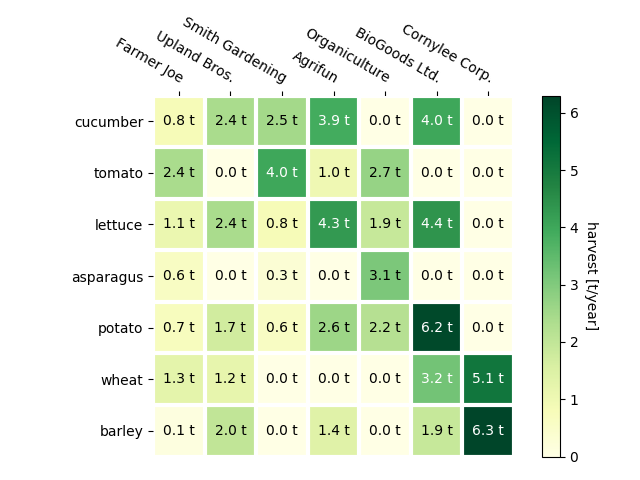
Los datos consisten en dos llaves (categóricas) y un atributo ordinal o cuantitativo. La marca es una área, y todas las arcas están separadas y alineadas en una matriz 2D. Los canales de posición mapean las categorías a posiciones x e y de cada área, y el canal de luminancia o saturación de cada área expresa el valor cuantitativo correspondiente. Esta codificación permite que el heatmap sea efectivo para encontrar outliers y clusters (basado en la similaridad entre filas y columnas). Su escalabilidad es flexible, pudiendo mostrar hasta 1 millón de áreas, cientos ed niveles categóricos, y aproximadamente 10 niveles en el atributo cuantitativo (veremos el por qué de este límite en la clase de colores).
En la clase de exhibición de proyectos vimos este heatmap creado en el Wall Street Journal sobre la aplicación de la vacuna para el sarampión en los Estados Unidos:
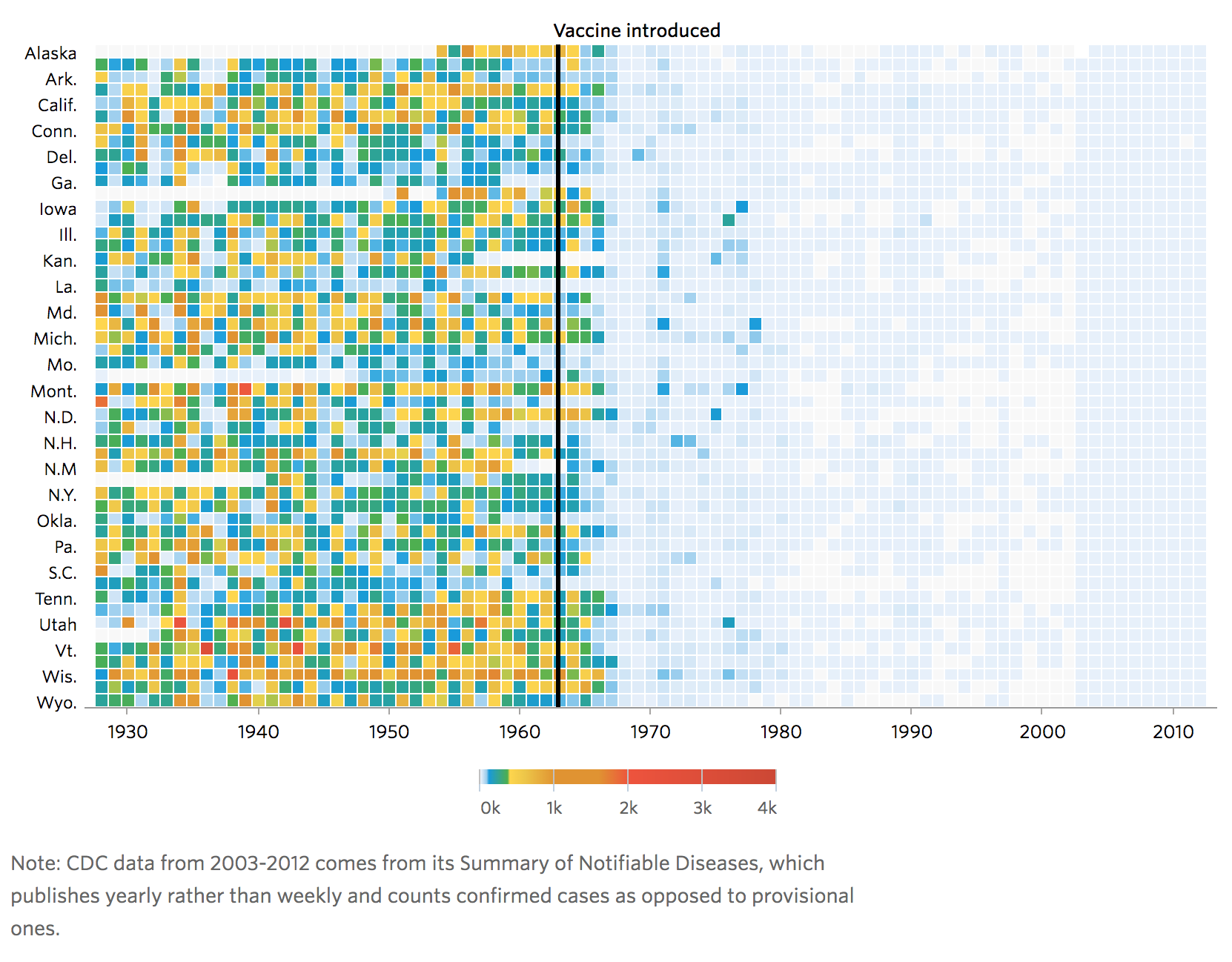
Este heatmap tuvo impacto, fue difundido y discutido por mucha gente alrededor del mundo. Entrega un mensaje claro. Y, lamentablemente, rompe el principio de expresividad, ya que utiliza un canal (tono) para un atributo cuantitativo. Sin embargo, eso no impide entender la visualización, porque el principal insight que se obtiene en ella es la distribución pre- y post-vacuna. Al observar la paleta de colores (particularmente la distribución de tonos en ella) podemos sugerir que el proceso de elección de esa paleta de colores fue deliberado, debido a la escasa presencia del tono celeste/azul, que sin embargo domina la matriz. ¡Quizás fue una manera de acentuar esa prominencia en el gráfico!
Cluster Heatmap #
La técnica clustermap extiende el heatmap de la siguiente manera: primero, se añade una tarea de derivar datos, que consiste en realizar clustering de las filas y las columnas del heatmap; segundo, se agrega una nueva marca, el dendrograma, un árbol que visualiza los resultados del clustering (son dos en total), utilizando líneas que determinan las conexiones jerárquicas de los clusters; finalmente, una marca extra que consiste en un área alineada con cada llave, cuyo tono identifica el cluster al que pertenece (esta marca es opcional, no siempre se utiliza). Como ejemplo, una red de zonas del cerebro se ve así en un ejemplo de la biblioteca seaborn
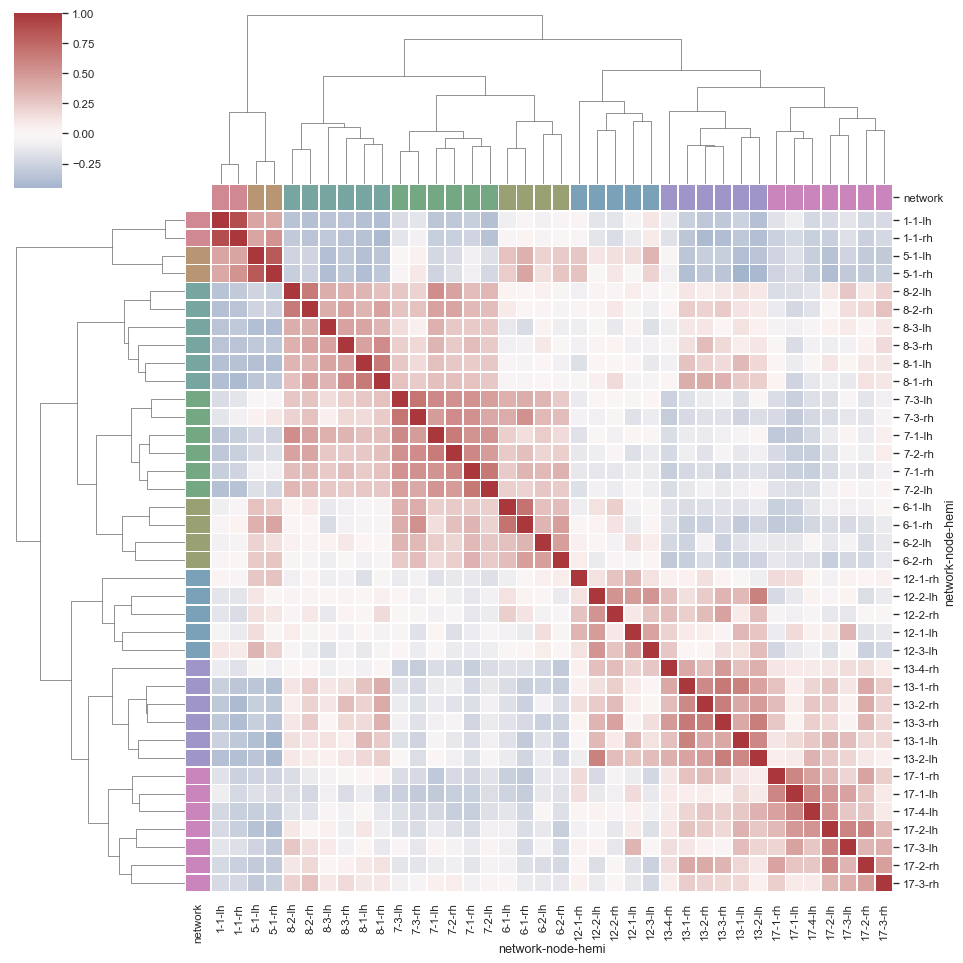
seaborn.
La propuesta del clustermap es que utiliza el clustering para (re-)ordenar las llaves de acuerdo a su posición en los árboles. Esto permite entender las relaciones grupales en el dataset de manera directa. También es utilizado en análisis exploratorio, con el fin de aplicar técnicas más avanzadas de clustering de manera posterior.
Scatterplot Matrix (SPLOM) #
Hemos visto gráficos space-filling que visualizan matrices, y gráficos de densidad que visualizan tablas de una dimensión. La técnica splom mezcla lo mejor de ambos mundos: ¡una matriz de visualizaciones scatterplot! La splom explora todos los pares posibles de atributos de una tabla con un scatterplot de cada uno de esos pares. Una tabla donde cada fila es un modelo de automóvil y sus atributos son caballos de fuerza (horsepower), peso (weight), aceleración (acceleration) y desplazamiento (displacement) se ve así:
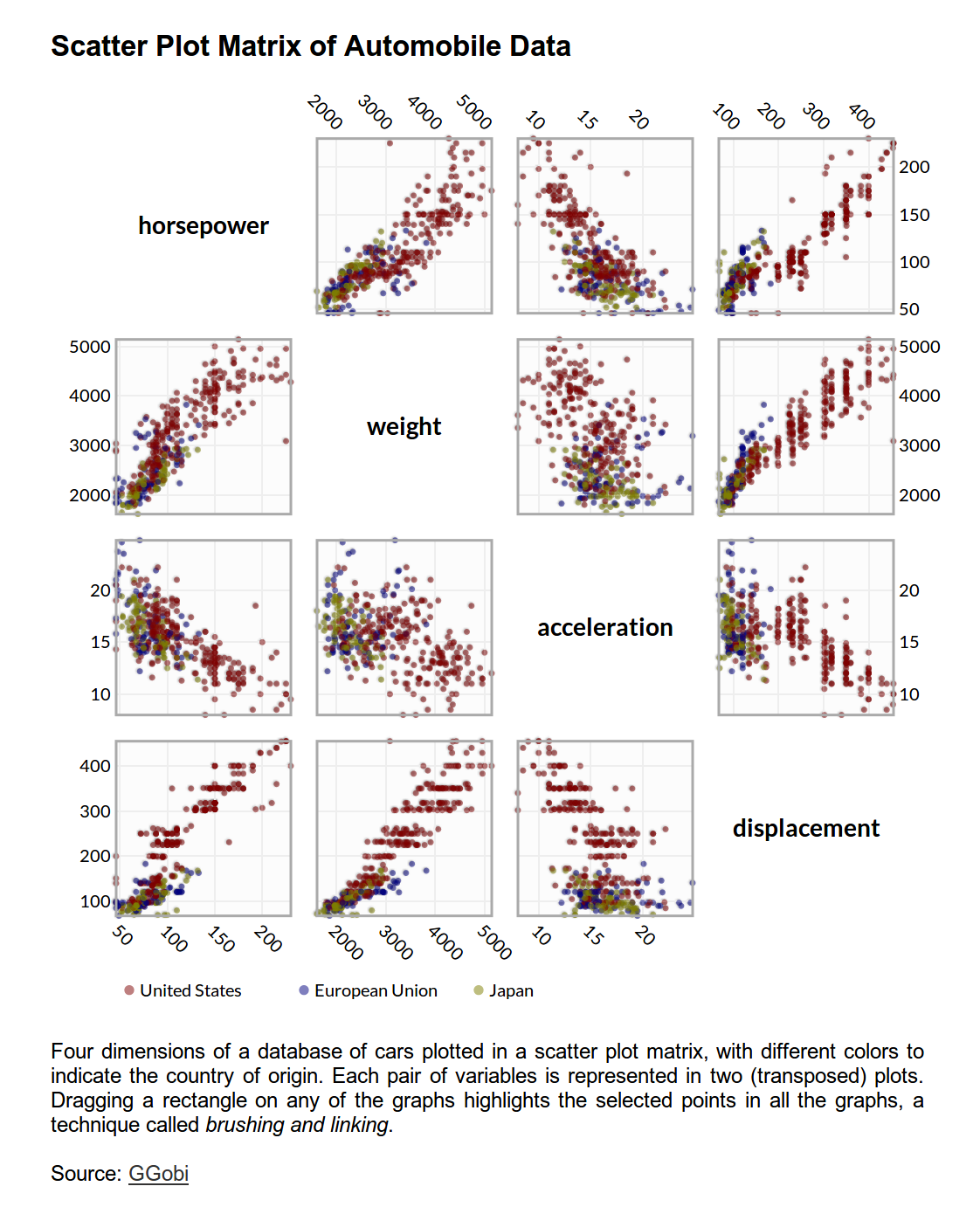
Observamos que cada scatterplot hereda la codificación visual del gráfico individual. La splom se suele utilizar para identificar pares de variables que presenten relaciones interesantes (de acuerdo a su correlación). Existen variaciones del gráfico, por ejemplo, se pueden mostrar los scatterplot solamente en la mitad superior o en la inferior, y utilizar un gráfico diferente en la otra mitad (puesto que los scatterplot son simétricos). También se puede utilizar la diagonal para mostrar un gráfico específico para cada variable (puede ser un gráfico de distribución, como un histograma).
La escalabilidad de la splom llega a la docena de atributos, y, como cada scatterplot puede ser pequeño, a decenas o cientos de ítemes.
Parallel Coordinates #
La técnica de coordenadas paralelas (parallel_coordinates), al igual que splom, se encarga de visualizar datos multidimensionales, particularmente múltiples atributos cuantitativos. Utiliza codificaciones visuales conocidas pero de una manera distinta. Hay dos tipos de marcas, las dos son líneas: primero, cada observación/fila/ítem de la tabla es una polilínea; segundo, cada atributo es representado por un eje. Los ejes pueden ser horizontales o verticales, pero solo puede haber un tipo de eje. Están dispuestos de manera paralela (por ello el nombre de la visualización), de modo que cada polilínea conecta los valores de cada atributo del ítem correspondiente. En el sitio Observable muestran un dataset de automóviles similar al de la visualización anterior, esta vez utilizando parallel_coordinates:
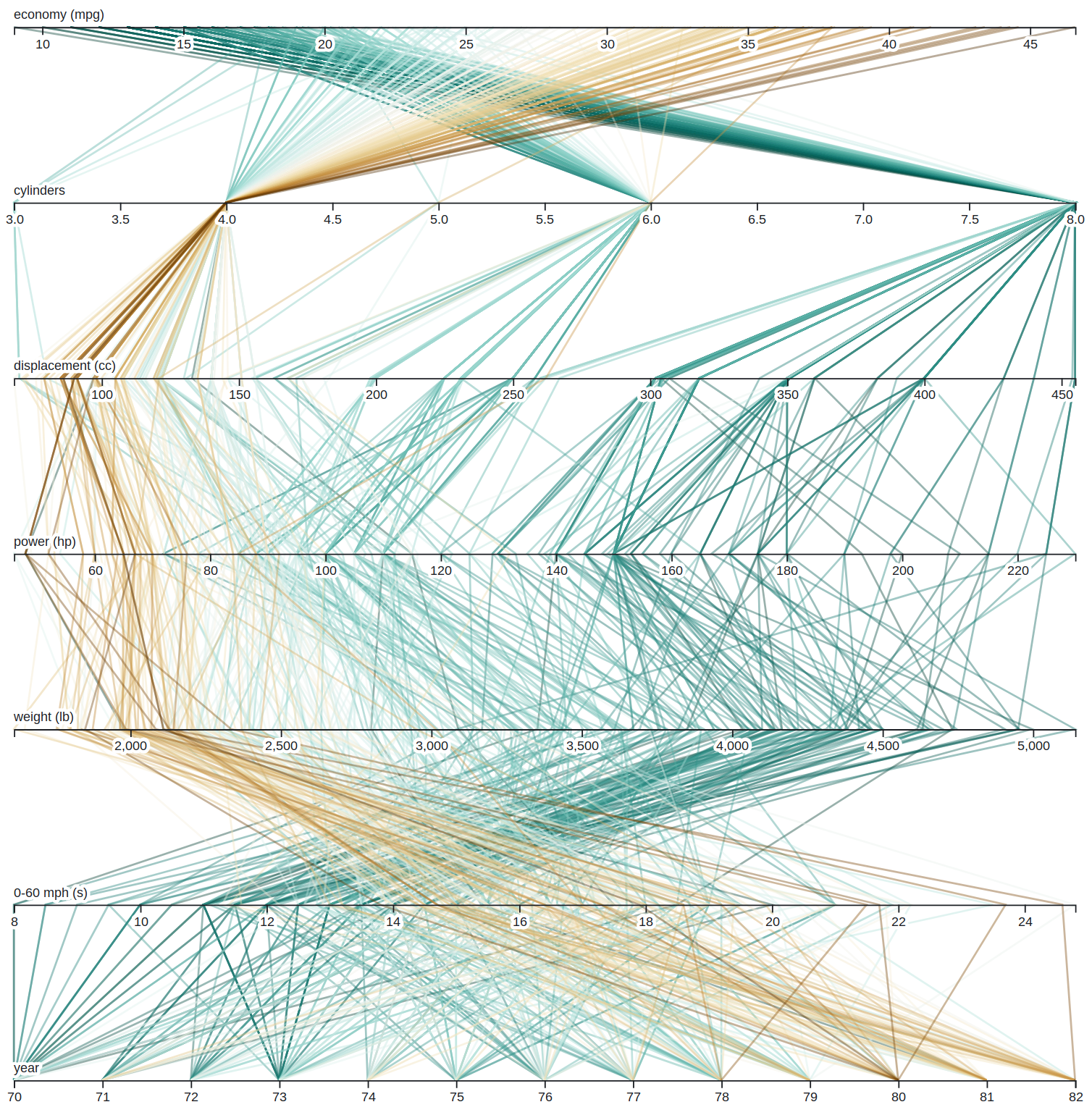
De acuerdo a la definición, cada línea es un automóvil. Además se utiliza el canal de tono de cada línea para identificar su valor de uno de los ejes, en el caso de la imagen, el atributo economy. Eso lo vuelve un canal redundante, pues economy es también un eje, sin embargo, darle color a las líneas facilita la interpretación del gráfico y la distinción de éstas.
Una dificultad en la interpretación de este gráfico es determinar el orden de los ejes. Dos ejes juntos permiten ver relaciones entre los dos atributos codificados en ellos, en función de las líneas que los conectan, pero se pierden las relaciones con los ejes que están más lejanos. Debido a eso, algunas implementaciones de parallel_coordinates permiten cambiar la posición de cada eje de manera interactiva.
El diseño de parallel_coordinates tiene una escalabilidad de decenas de atributos y cientos de ítemes.
Pie y Polar Area charts #
Otros clásicos de la visualización (y cómo no decirlo, controversiales también) son el pie_chart y el polar_area_chart. Ambos tienen apariencias similares y utilizan ejes radiales, pero utilizan canales distintos. Son gráficos basados en ángulos, que visualizan un atributo llave categórico y un atributo cuantitativo. En ambos la marca es un área que nace en un círculo y que tiene un radio y ángulo. La siguiente imagen muestra ambos gráficos:
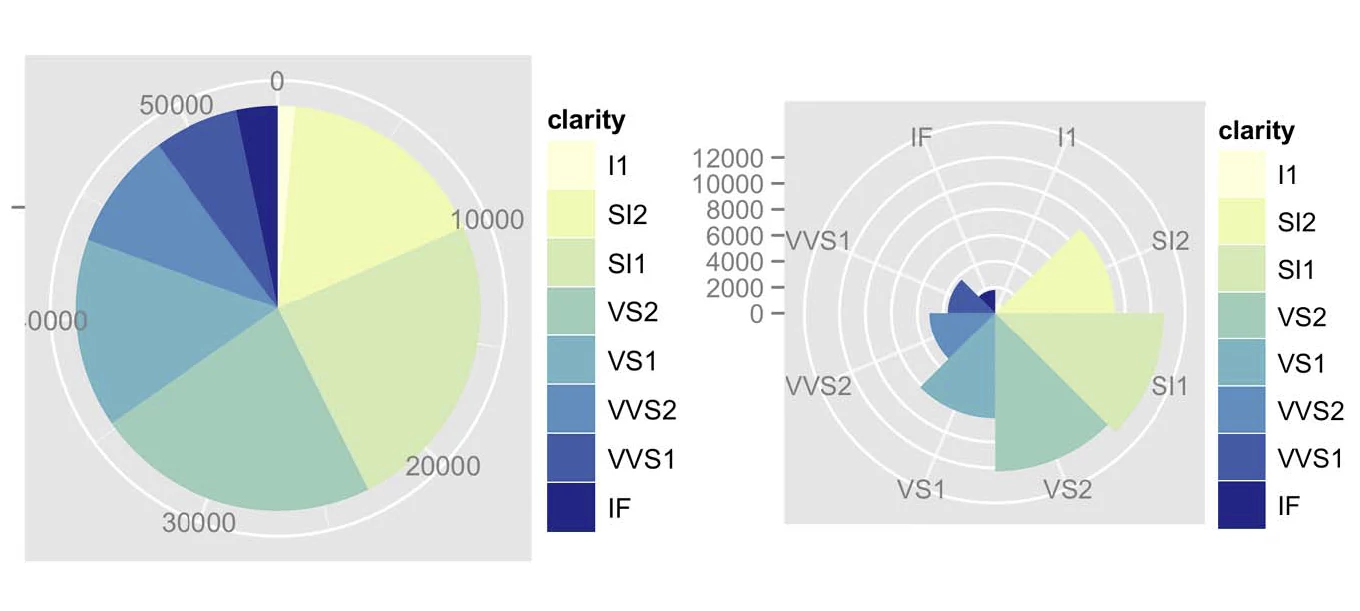
Las diferencias en los canales son las siguientes:
pie_chart: todas las marcas tienen el mismo radio. El canal angular codifica el valor cuantitativo.polar_area_chart: todas las marcas tienen el mismo ángulo. El canal radial (por tanto, área) codifica el valor cuantitativo.
En ambos el tono codifica la llave categórica. Las tareas que se pueden realizar con estas visualizaciones son la comparación de relaciones y el entendimiento de parte-de-un-todo. Sin embargo, ángulo y área son canales menos precisos que el largo de una línea o barra para realizar comparaciones.
Comparando estos gráficos con otras técnicas, la disposición circular implica que se necesita un área de gran tamaño para entender las relaciones, lo que podría utilizar mucho espacio en comparación con otras alternativas basadas en barras (que pueden ser rectángulos delgados): un pie_chart es el equivalente de un glifo de barras apiladas en el normalized_stacked_bar_chart, un polar_area_chart es el equivalente de un bar_chart.
Box Plot #
Las técnicas que hemos visto en esta unidad trabajan directamente con la tabla a visualizar. Ahora bien, existen ocasiones en las que no necesitamos ver cada elemento de la tabla, sino que la tarea es encontrar la distribución de grupos dentro de la tabla, y comparar dichas distribuciones.
Ésa es la funcionalidad de un box_plot, que agrega los ítemes de una tabla, como se ve a continuación:

Este box_plot muestra los resultados de distintos experimentos (numerados del 1 al 5) para medir la velocidad de la luz. Cada experimento cuenta con múltiples medidas, de modo que se puede mostrar una distribución de la velocidad en cada experimento. Como dice su nombre, el box_plot está basado en cajas (boxes). Cada caja es un glifo que expresa los siguientes datos derivados de la tabla: la mediana (línea central en la caja, con mayor grosor de línea); los cuartiles inferior y superior (límites de la caja); los límiites inferior y superior, definidos usualmente como una medida del IQR, que muestran los límites de datos no outliers en la distribución (Inter Quartile Range, o rango entre cuartiles); y finalmente los outliers, que están tan lejos de los demás elementos que se representan como puntos alejados de la caja. Todas las posiciones de estas marcas utizan el canal de posición y de largo (en el caso de la caja) para expresar sus valores.
Hoy este gráfico sigue siendo utilizado para comparar distribuciones y encontrar outliers, tanto en análisis exploratorio como en tareas específicas. Ahora bien, los box_plot fueron diseñados en una época en la que las visualizaciones se hacían con papel y lápiz, por tanto tienen defectos derivados de los límites del medio original. El principal es que omiten características relevantes de las distribuciones de los datos. Existen alternativas más modernas que modifican las marcas para que incluyan información de las distribuciones:
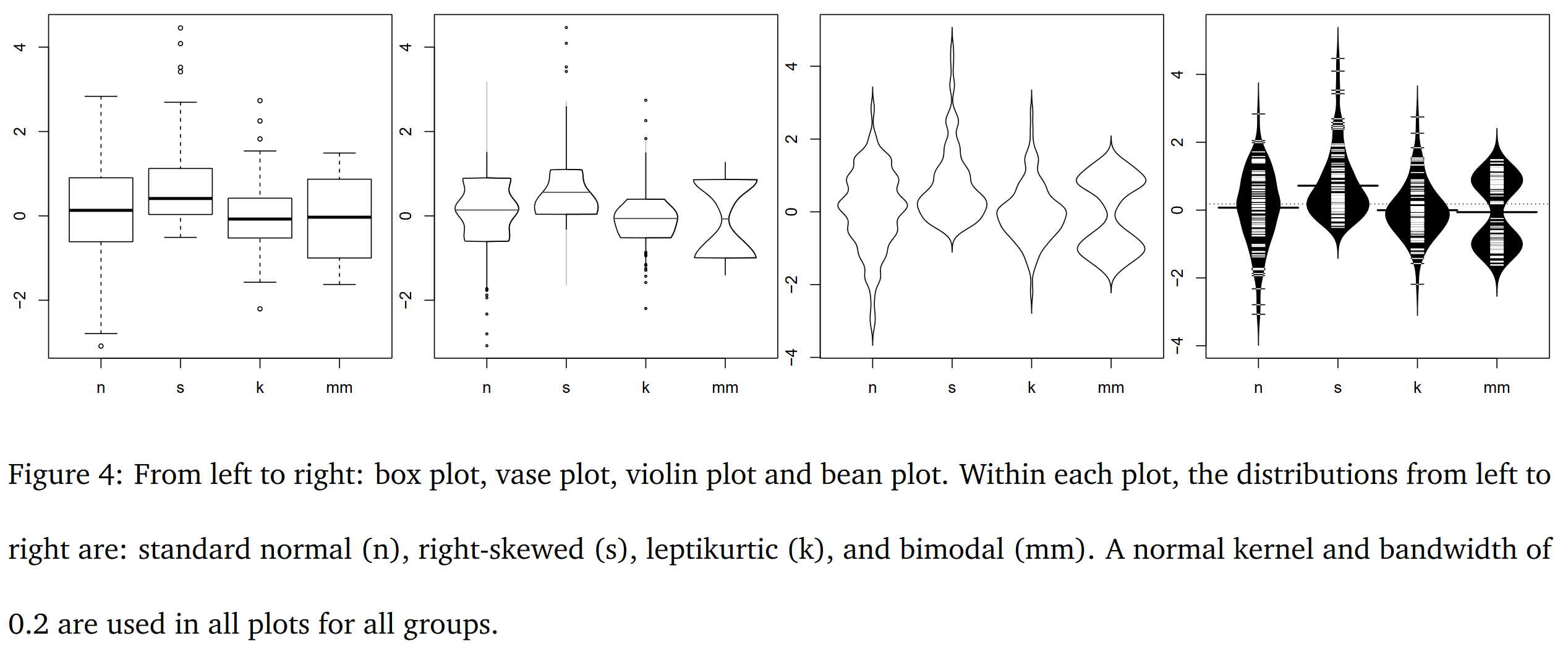
box_plot. Fuente: 40 years of boxplots, Wickam & Stryjewski.
Las alternativas que muestra el gráfico son el gráfico de vasija, el violin_plot y el bean_plot. Estas técnicas (y otras) suelen estar presentes en los módulos de visualización. Aún así, los box_plot se siguen utilizando. Tienen un aspecto familiar y simple de interpretar, mientras que las alternativas requieren derivar la distribución — y eso hace que surjan preguntas respecto a los métodos de derivación. Antes de elegir una alternativa es importante conocer a la audiencia del gráfico y las propiedades de nuestros datos.
Qué llevarse para la casa #
La mayoría de las visualizaciones en esta unidad son conocidas o al menos familiares. Incluso algunas las hemos utilizado en Python. Lo que ha cambiado es la manera de describirlas y definirlas, utilizando nuestro marco conceptual de marcas y canales. Al analizar cómo se define una visualización en función del qué se visualiza (los datos), el para qué (la tarea) y el cómo (la codificación), hemos ganado conocimiento que nos permitirá tomar mejores decisiones en nuestros proyectos. Este proceso de decisión no es fácil ni simple, sin embargo, una vez que tengan práctica, comenzarán a ver la ciencia de datos con otros ojos, al poseer nuevas maneras de observar y analizar.
Lecturas Recomendadas #
- Collins, Christopher, Gerald Penn, and Sheelagh Carpendale. Bubble sets: Revealing set relations with isocontours over existing visualizations. IEEE Transactions on Visualization and Computer Graphics 15, no. 6 (2009).