¿Qué visualizar? Abstracción de Datos

La base de la visualización son los datos que se van a visualizar. Por ello, el primer paso para aprender a visualizar es establecer las bases que definen qué es un dato.

Usualmente, cuando se tiene un conjunto de datos se habla de dataset. Un dataset puede estar en una base de datos, en uno o más archivos en algún formato específico, o puede estar distribuido en múltiples máquinas y formatos. El almacenamiento de los datos no es un tema que nos preocupe. Un dataset se define así:

Un dataset es un conjunto de observaciones, registros, etc., que contiene variables y atributos, usualmente numéricos.

En este curso no discutiremos las maneas de almacenar datos. Nos enfocaremos en cómo representarlos visualmente para realizar tareas y resolver problemas. Por ello, lo que sí nos concierne es la estructura que tienen los datos, tanto en su organización (tipo de dataset) como en sus atributos (variables de cada observación).

En esta unidad veremos que existen distintos tipos de datasets. Para cada tipo veremos proyectos de visualización de ejemplo. Luego, definiremos los tipos de atributos que pueden encontrarse en los datos.

Tipos de Dataset #

Trabajaremos con una categorización general que define cuatro tipos: tablas, redes y árboles, campos, y datos espaciales.

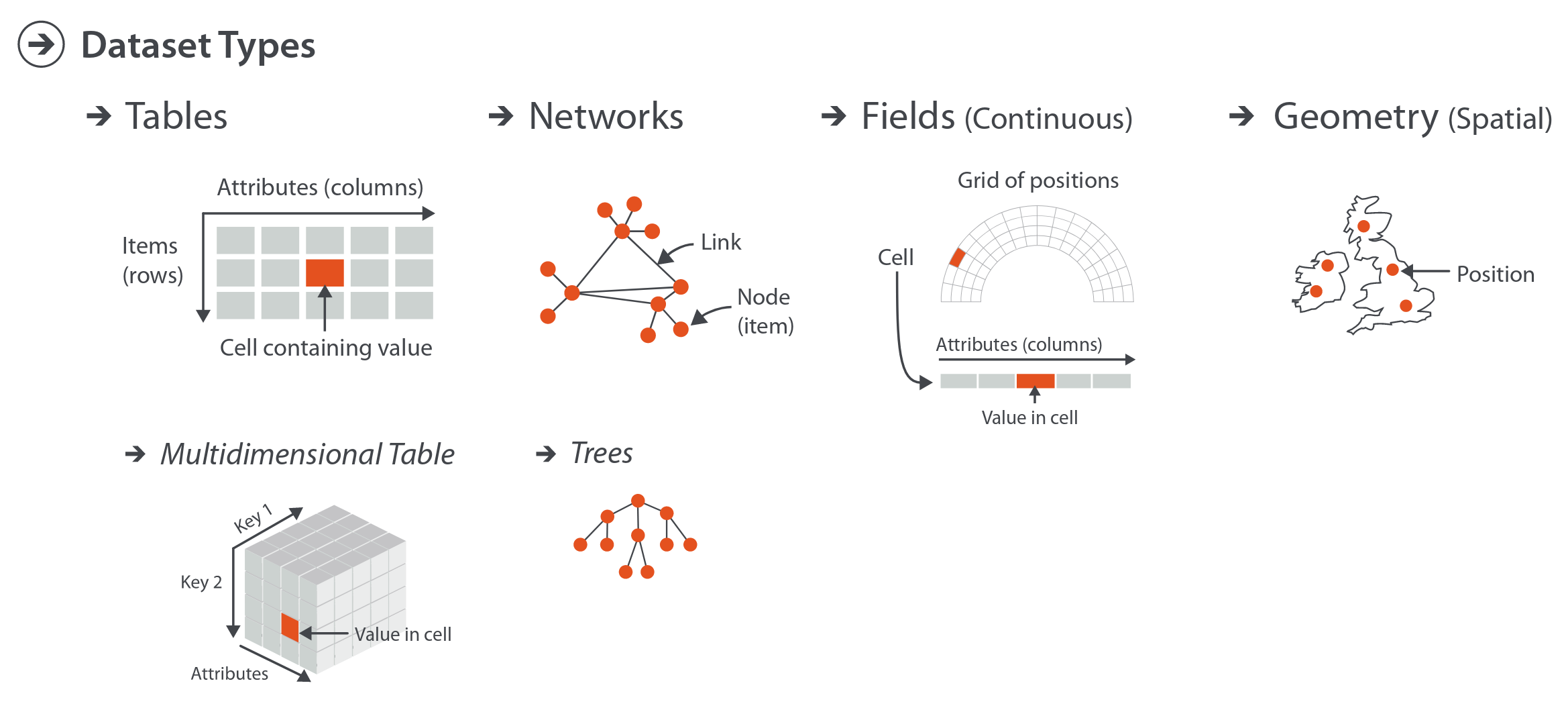
En casos complejos, cualquier tipo de dataset se puede expresar como una combinación de estos tipos de datos. A continuación definiremos cada dataset, mencionaremos las operaciones que se pueden realizar con ellos, y veremos ejemplos para cada uno.

Tablas #

En una tabla las observaciones se organizan en filas, mientras que sus características se organizan en columnas. Es un dataset base, en tanto todo lo podemos expresar como una tabla, aunque no sea óptimo para la semántica del dato que estemos analizando.

Seguramente todes hemos visto o usado tablas:

• La tabla de posiciones del campeonato de fútbol es… una tabla.
• El estado de cuenta de tu cuenta en el banco es una tabla.
• Una hoja de cálculo (spreadsheet) es una o más tablas.
• Una matriz es una tabla. En Machine Learning, una feature matrix es una tabla que cumple esta definición.

La definición de una tabla no se limita a dos dimensiones. Una tabla puede ser multidimensional. En dicho caso, en vez de ser una matriz, es un tensor. Ahora bien, no todo lo que tenga forma de tabla es una tabla. Un bingo no es una tabla, porque no tiene la semántica de observaciones en filas y variables en columnas.

En Python utilizaremos un DataFrame de pandas como una tabla. Esto permite que cada observación (fila) tenga un identificador (que se almacena en un índice), y cada columna tenga un nombre.

Las operaciones que se pueden realizar en una tabla son las siguientes:

• Filtrado: una tabla filtrada contiene un subconjunto de las observaciones de la tabla original, de modo que cada observación del subconjunto cumple con un criterio específico, como que una variable tenga un valor específico.
  • Por ej., de la tabla de clientes, quiero los que pertenecen al programa gold de nuestra compañía.
  • En pandas se expresa así: dataframe[dataframe[variable] == valor].
• Agrupación: la agrupación de una tabla se define de acuerdo a una o más columnas para agrupar. En esas columnas se determinan los valores posibles que adquiere cada columna, y por cada valor (o combinación de valores, en caso de ser varias columnas) se obtiene una tabla filtrada para ese (esos) valor(es).
  • Por ej., quiero agrupar la tabla de viajes de acuerdo al modo de transporte utilizado. Como resultado, tengo una tabla por cada modo de transporte.
  • En pandas se expresa así: dataframe.groupby(columna).
• Agregación: la agregación de una tabla implica calcular un valor derivado del total de valores de una o más columnas. El ejemplo más común es calcular el promedio de cada columna.
  • En pandas el promedio de una tabla se expresa así: dataframe.mean().

Lo común es aplicar estas operaciones en conjunto. Como ejemplo: se filtra la tabla de viajes para obtener los viajes desde el hogar al trabajo, luego se agrupa por modo de transporte, y finalmente se calcula (agrega) el tiempo de viaje promedio de cada grupo. Como resultado, se obtienen las diferencias de los promedios en ese tipo de viaje entre los distintos modos de transporte disponibles en la ciudad.

Ejemplo: Censo 2017 (Chile) #

Un censo genera una tabla donde cada fila es una persona y cada columna es una variable asociada a cada persona. Si se carga en censo 2017 de Chile en pandas se ve algo así:

Algunas columnas representan meta-datos, como la región o el identificador de la comuna, o la edad de la persona. Otras representan las preguntas del censo.

Un ejemplo de filtrado->agrupación->agregación se ve en la siguiente visualización. Primero, filtré a las personas migrantes (dejando fuera a las nacionales), luego agrupé por lugar de origen (la columna P12PAIS_GRUPO). En cada grupo calculé la proporción de personas que llegó en cada año al país.

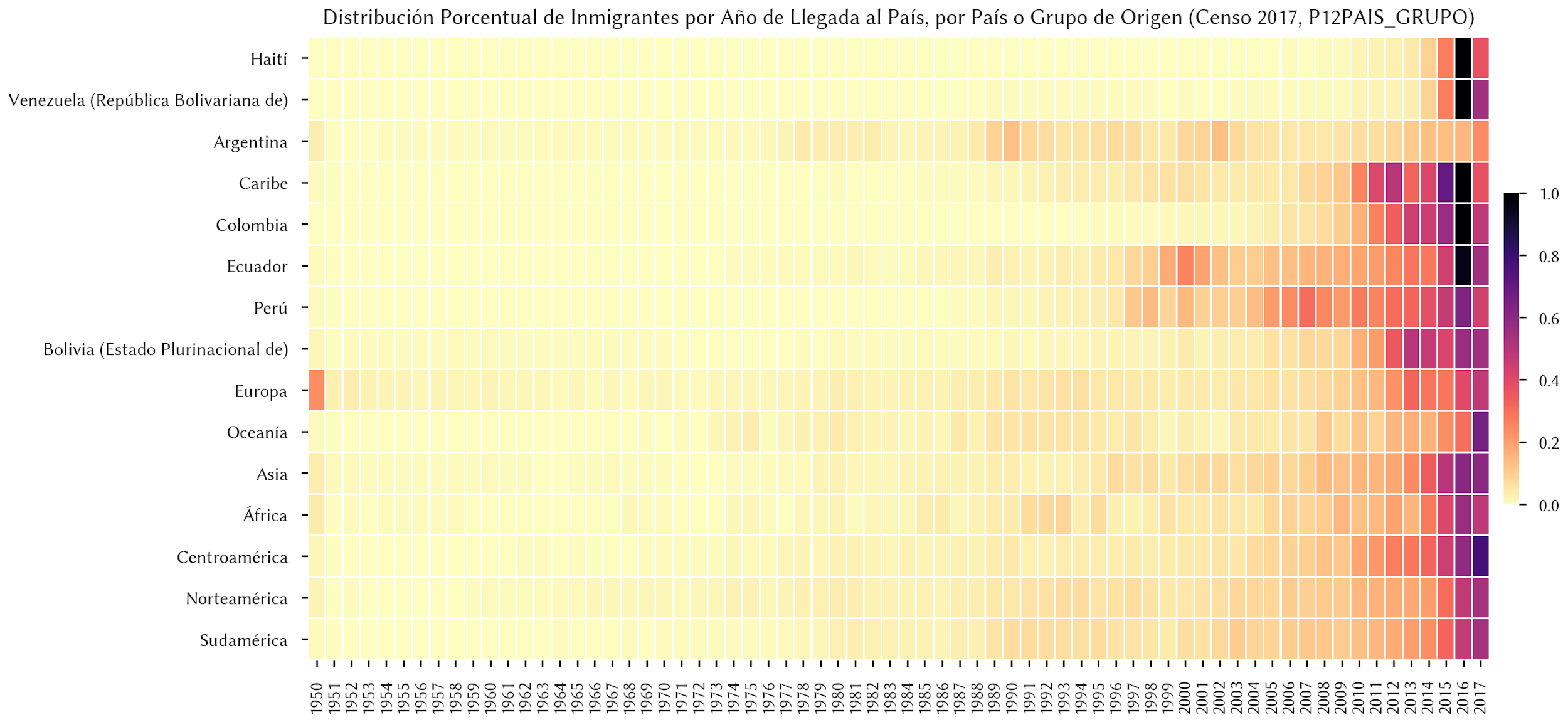
El código fuente de este ejemplo está en este repositorio.

Cuando hablamos de tablas, solemos obviar lo que significa una observación. Por ejemplo, en el censo cada persona es una observación – ¿qué pasaría si considerásemos cada respuesta como una fila? Todo dependerá de lo que querramos resolver. Una lectura sugerida al respecto es Tidy data de Hadley Wickham (publicado en el Journal of Statistical Software), donde explica como organizar tablas. Esta organización es importante para nosotres ahora porque muchos métodos de seaborn asumen que los datos vienen en formato tidy.

Redes y Árboles #

En una red las observaciones son nodos. Y cada nodo puede estar conectado con otros, y en una cantidad arbitraria — puede ser con otro nodo, con muchos más, o con ninguno. Estas relaciones se representan con aristas o enlaces (links). Tanto nodos como links pueden tener atributos. Un link puede ser dirigido (va desde A hasta B, es decir, A -> B, distinto de B -> A), no dirigido (el link A -> B es equivalente a B -> A), o múltiple (pueden existir distintos links A -> B, cada uno con sus propios atributos).

Existen muchos datasets de redes, como los provenientes de una red social, donde los nodos son personas, y los links son relaciones de amistad u otro tipo (dependiendo de la red), o una red de transporte, donde los nodos son paraderos, estaciones de metro y esquinas, y las aristas son las calles que conectan dichos nodos.

En Python se suele utilizar la biblioteca networkx para trabajar con redes. Es directa de usar ya que utiliza estructuras de Python para representar cada red. Por lo mismo es ineficiente en desempeño. Otras bibliotecas son mejores en ese aspecto, como igraph y graphtool, sin embargo, son más difíciles de usar. En el curso usaremos networkx.

Un árbol también es una red, ya que tiene nodos y links entre nodos. La diferencia es que tiene restricciones: el árbol comienza en un nodo, llamado raíz (root). La raíz tiene links dirigidos hacia otros nodos, que a su vez tienen links hacia otros nodos, creando una jerarquía de niveles. Los nodos en el último nivel, que no tienen links hacia otros nodos, son conocidos como hojas (leaves). Con esta definición, todo árbol es una red, pero no todas las redes son árboles.

Las operaciones más comunes en redes son las siguientes:

• Cálculo de importancia de nodos y aristas. Esto se suele conocer como centralidad. Por ejemplo, la degree_centrality define que la importancia de un nodo está dada por la cantidad de enlaces que recibe.
• Determinación de un camino entre nodos. Se suele preguntar por el camino más corto entre A y B. Pero la definición de más corto puede ser diversa, no es necesariamente distancia física o distancia entre conexiones. Como los links pueden tener variables, se puede calcular una distancia basada en ellas.
• Detección de Comunidades. Los nodos de una comunidad están más conectados entre sí que con los nodos fuera de la comunidad. ¿Cómo detectar esto? Existen numerosos enfoques, algunos más modernos que otros. El más común es conocido como Louvain.
• Predicción de atributos. En ocasiones no conocemos los atributos de un nodo, pero sí conocemos los de quienes lo rodean. Eso permite predecir los atributos que no conocemos si se dan las circunstancias correctas.

Hay toda un área de investigación llamada Network Science. El libro del mismo título de uno de los pioneros en el área, Albert-László Barabási, está disponible libremente en la red.

Ejemplo de Red: Atlas de Complejidad Económica del MIT Media Lab #

Este proyecto liderado por César Hidalgo busca crear un mapa del desarrollo económico en el mundo, entre otros aspectos. Una de las maneras de hacerlo es ilustrando el conocimiento y la generación de valor a través de los productos y servicios exportados e importados por las naciones. En el siguiente ejemplo, un nodo es un producto o servicio, y dos nodos están conectados si son producidos por el mismo país. Un atributo de un nodo es la industria a la que pertenece (Minería, Agricultura, Tecnología, etc.).

A través de esa definición de la red, se puede obtener el siguiente mapa:

Cada nodo es coloreado de acuerdo a la industria a la que pertenece. Esto permite que veamos el tamaño de cada industria y la complejidad de ésta, basándonos en las conexiones entre productos. Si nos abstraemos de los nodos y nos fijamos en esas comunidades, podremos ver cuales comunidades están conectadas entre sí, y cuáles son opuestas.

También vemos cuál es el camino que se debe recorrer para poder llegar desde producir un producto A hasta un producto B. Por ejemplo, Chile produce cobre, pero si quisiera producir computadores, tendría que desarrolar al menos todo el conocimiento implícito entre los productos que están en el camino cobre -> ... -> computadores.

En el ejemplo se destacan con un borde negro los productos que son exportados por Guatemala. Eso permite conocer directamente cuáles son las industrias en las que participa (o no) ese país. Al mismo tiempo, elegir otro país permitiría comparar sus producciones.

Pueden explorar una versión actual de esta red, para Chile, en: https://atlas.media.mit.edu/en/profile/country/chl/-

Ejemplo: Visualizando un Árbol de Decisión #

Un algoritmo clásico de Machine Learning es la creación e inferencia de árboles de decisión para clasificar datos. Estos árboles presentan secuencias de decisiones estructuradas como árboles, y son los pilares de algoritmos más avanzados y modernos para clasificar datos.

El siguiente ejemplo muestra como se ve un árbol de decisión:

No solo eso, el sitio también muestra como se utiliza este árbol para clasificar datos a través de interacción y animación. Vean la demostración de esta animación en: http://www.r2d3.us/visual-intro-to-machine-learning-part-1/.

Campos #

El tipo de dataset campo se refiere a aquellos datos que modelan fenómenos que son continuos en un espacio (no necesariamente un espacio real). Ser continuo significa que entre un punto y otro hay infinitos puntos, por ejemplo, la temperatura o la presión de un entorno (como una habitación) se pueden leer en cualquier punto de éste, y es probable que distintos puntos tengan distintas mediciones. Este campo continuo puede ser discretizado en una grilla — una habitación puede ser dividida en múltiples cubos pequeños, en el cual se asume que la temperatura o la presión tienen un valor uniforme dentro de ese cubo.

Una grilla puede ser regular (como un conjunto de cubos) o irregular (con cada elemento de la grilla con una forma propia). Estos datasets usualmente provienen de simulaciones, modelos de fenómenos físicos, sensores, etc.

Entre las operaciones que se realizan con campos están:

• Estimación de valor. Queremos saber el valor del campo en un celda de la grilla, o bien la distribución de este valor en la grilla (una parte o completa).
• Estimación de variación y caminos. No siempre se trabaja con campos estáticos. En ocasiones, también se visualizan cambios o flujos dentro de los campos, es decir, la diferencia del valor entre una celda y sus celdas vecinas. Por ejemplo, el flujo de aire alrededor de una turbina, o el flujo electromagnético sobre un metal.

Existen distintas maneras de visualizar campos. A continuación se muestran alternativas para las operaciónes de estimación de variación y caminos:

¿Cuál de estas alternativas es mejor? No podemos responder esto a priori, puesto que necesitamos conocer la tarea a resolver y la audiencia que hará uso de la visualización.

Ejemplo: Mapa de Viento #

El viento es un campo infinito que tiene dirección y cambia constantemente. Los investigadores Fernanda Viegas y Martin Wattenberg tomaron sensores de viento en tiempo semi-real de los Estados Unidos y produjeron la siguiente visualización interactiva:

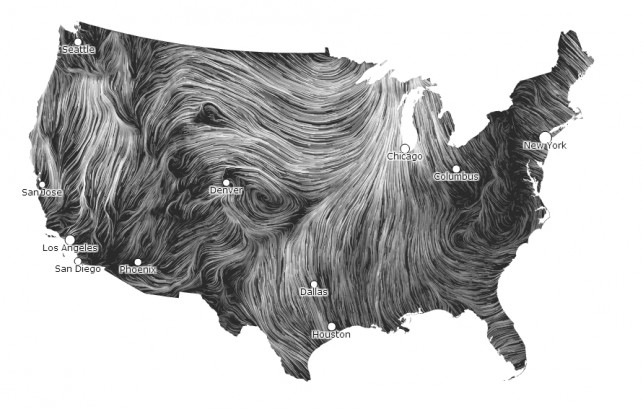
No solo es un espectáculo verla, sino que ha sido utilizada para analizar fenómenos climáticos en el país. Pueden verla en todo su esplendor aquí: http://hint.fm/wind/.

Datos Geográficos y Espaciales #

Este tipo de datos contiene observaciones y atributos que tienen una representación directa. En el caso de los datos geográficos, los mapas muestran (usualmente) toda o buena parte de la información disponible. Un mapa suele ser bidimensional, al observar el terreno o una ciudad desde un punto de vista específico, usualmente superior. En cambio, los datos espaciales pueden ser tridimensionales, e incluso tener volumen (contenido interior). Tal es el resultado de un escáner que crea una imagen en 3D del cuerpo humano, concretamente, de su interior.

En este curso nos enfocaremos en los datos geográficos. El trabajo con datos de volumen suele ser especializado, pero el enfoque del curso es general.

Las observaciones en este tipo de datos consisten en un conjunto de elementos, usualmente categorizados así:

• Puntos. Un punto tiene posición 2D o 3D, pero no tiene volumen, superficie ni largo.
• Líneas o Conjuntos de Líneas. Una línea conecta dos puntos. No tiene volumen ni superficie, pero tiene largo.
• Áreas. Las áreas están determinadas por cortes planares conformados por líneas o conjuntos de líneas. Estos polígonos (o conjuntos de polígonos) tienen área, pero no tienen volumen.
• Superficies. Podrían ser equivalentes a las áreas en su representación (en caso de usar polígonos), pero existen superficies que teóricamente no están determinadas por líneas, como la superficie de una esfera. Ahora bien, esta superficie de esfera está hueca, no considera volumen.

Un ejemplo de un mapa que representa información geográfica de manera directa es el siguiente:

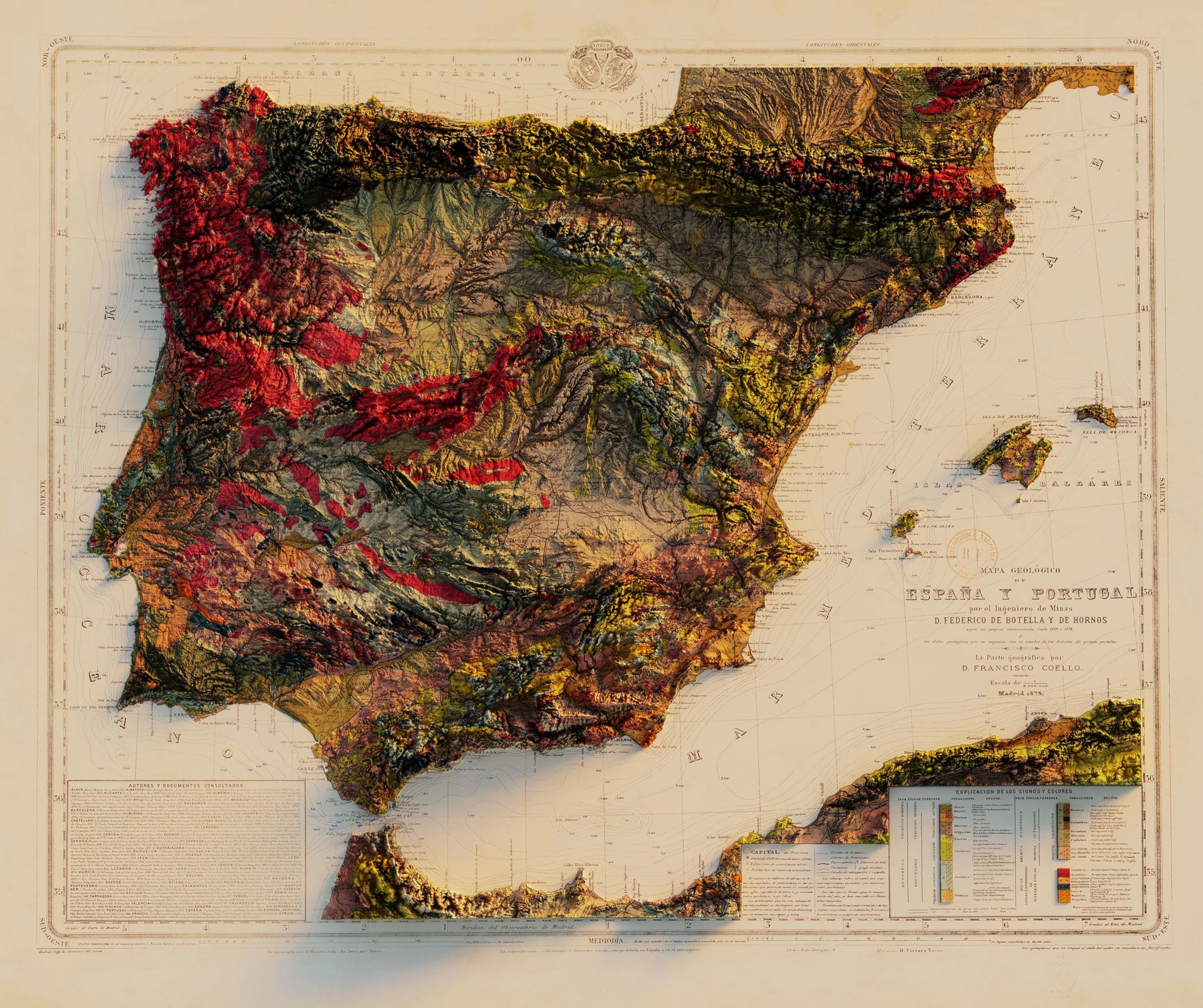
Es un mapa precioso, de un proyecto que recrea mapas vintage utilizando herramientas modernas. Sin embargo, cuando visualizamos, buscamos realizar operaciones que no son necesariamente eficientes o posibles cuando se utiliza tanto detalle. ¡Todo depende siempre de la tarea a realizar! Entre las operaciones que podemos hacer con mapas se encuentran:

• Encontrar. Necesitamos saber la ubicación de un elemento conocido.
• Comparar. Queremos medir las diferencias y similitudes entre elementos que están en posiciones distintas. Por ejemplo, ver el contexto hídrico y montañoso de dos ciudades.
• Explorar. No es necesario tener una pregunta para ver un mapa. La exploración libre de éste nos ayudará a comprender el contexto de los datos y a generar nuevas preguntas.
• Contextualizar. Podemos darle contexto geográfico a los datos que tengamos. Un ejemplo: conocer los atributos y distribución geográfica de las personas en el censo.

Una característica de los mapas como representación de datos geográficos es que prácticamente a todas las personas le son familiares (en cierta medida). Eso facilita la comunicación y la resolución de tareas.

En Python utilizaremos la biblioteca geopandas para cargar, procesar y visualizar información geográfica. Al ser una biblioteca que extiende pandas, su uso nos será familiar. Además utilizaremos la biblioteca PySAL (Python Spatial Analysis Library), que, como dice su nombre, nos permitirá realizar análisis espacial en pos de las visualizaciones que necesitemos hacer.

Ejemplo: Censo 2017 de Chile #

Retomemos los datos del censo y démosle contexto geográfico. El siguiente mapa muestra la proporción de inmigrantes en cada distrito censal del radio urbano de Santiago:

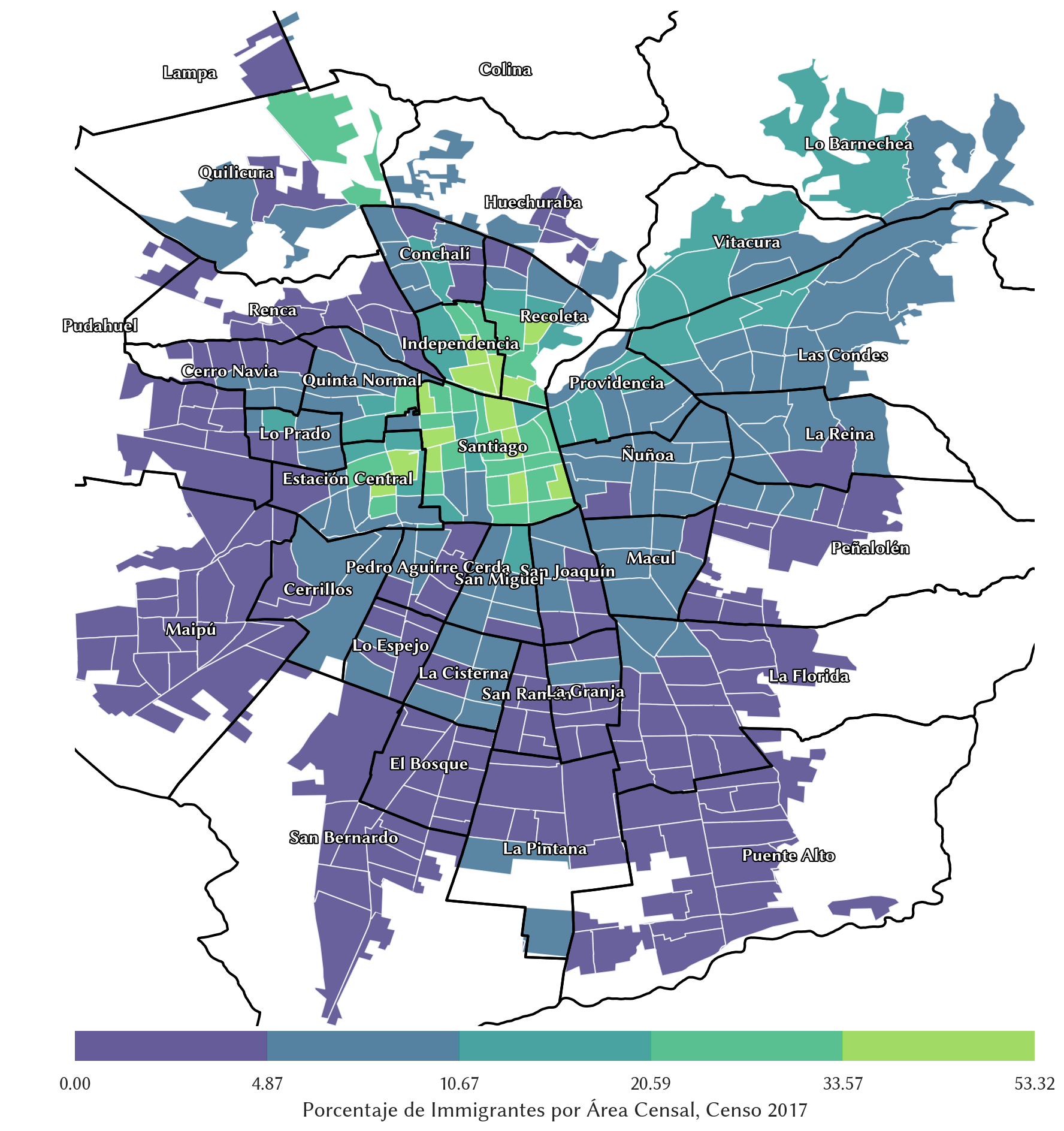
En el mapa observamos los bordes administrativos de cada distrito censal, los bordes administrativos de cada comuna, y el nombre de cada comuna. Esa es información geográfica que se despliega directamente y que da contexto — al colorear cada distrito de manera que el color codifique la proporción de inmigrantes, el mapa nos permite saber cuáles distritos son vecinos, si hay similitud en la proporción de inmigración entre distritos cercanos, y dónde se encuentran los clusters o grupos de distritos que concentran mayor inmigración.

¡Tipos de Dataset no son Excluyentes! #

Un dataset puede contener una mezcla de tipos. Pr ejemplo, una red de transporte también tiene componentes geográficas. Como vemos en el ejemplo que sigue, esto abre posibilidades: se puede utilizar la red y la geografía para calcular posiciones abstractas basadas en otras variables, como el tiempo total de viaje. La siguiente visualización muestra como se compara el tiempo de viaje entre estaciones en distintas componentes de la red de metro de Nueva York, partiendo desde la estación en Manhattan.

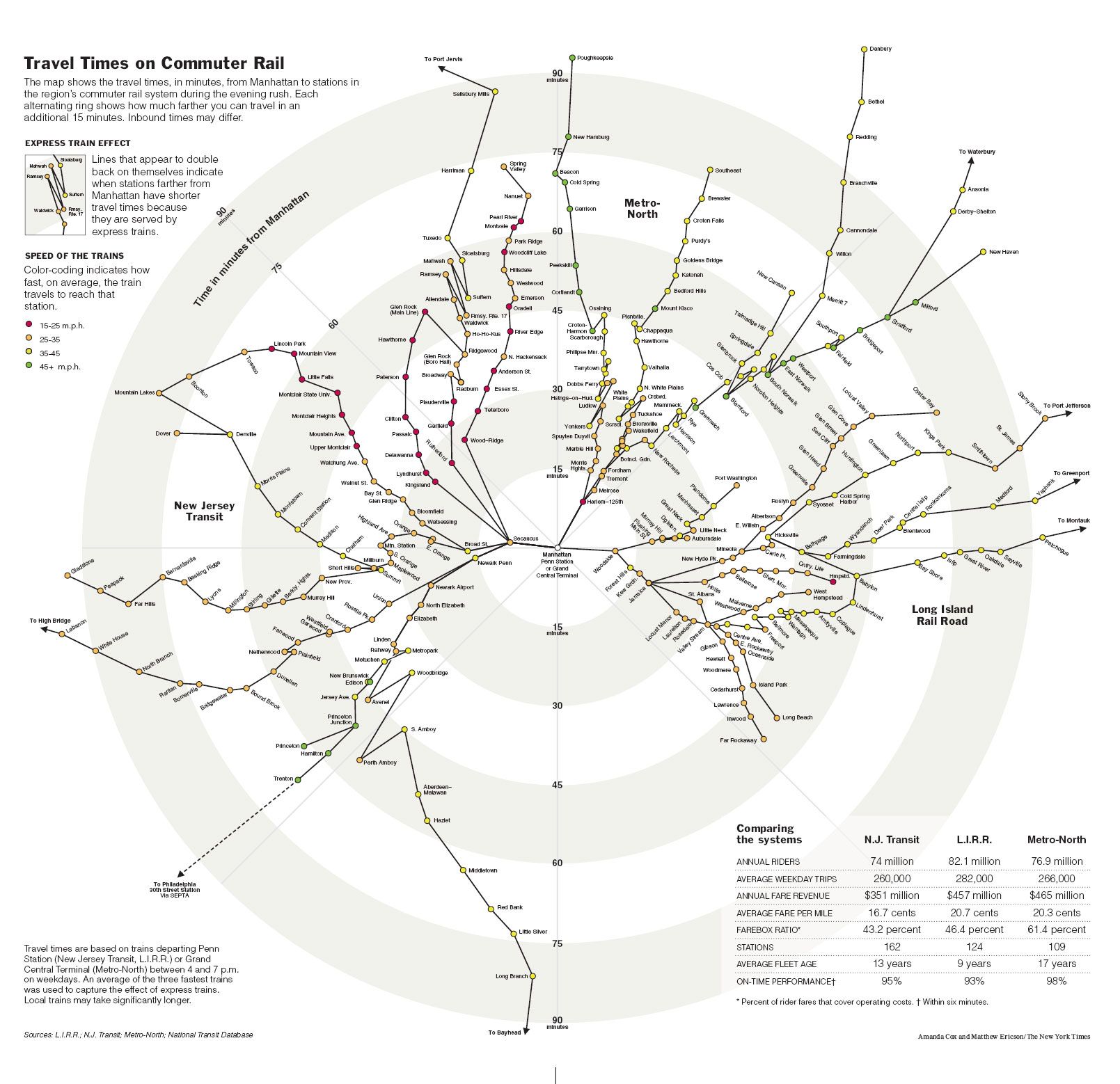
Al no utilizar las posiciones geográficas de las estaciones, sino que derivar una posición en la visualización a partir del operador de la línea de tren (son varios operadores) y del tiempo de viaje para llegar a cada estación (es un gráfico radial, a medida que se aleja del centro, es mayor tiempo de viaje), es posible comparar la complejidad y rapidez de distintas líneas del tren.

No es una visualización directa de ver. Por ello también incluye leyendas y notas que la explican. Es una visualización para zambullirse y explorar en profundidad.

Atributos #

Hasta este momento hemos hablado de la organización y semántica de cada tipo de dataset, con un énfasis en sus observaciones, ítems, registros, etc. Cada observación tiene atributos, por ejemplo, en el censo cada columna de la tabla era un atributo asociado a cada persona. Pero no especificamos si cada una de esas columnas, que definimos como atributos, y que también solemos llamar variables, también siguen una especificación. Ciertamente la siguen. Los tipos de atributos con los que trabajaremos se exhiben a continuación:

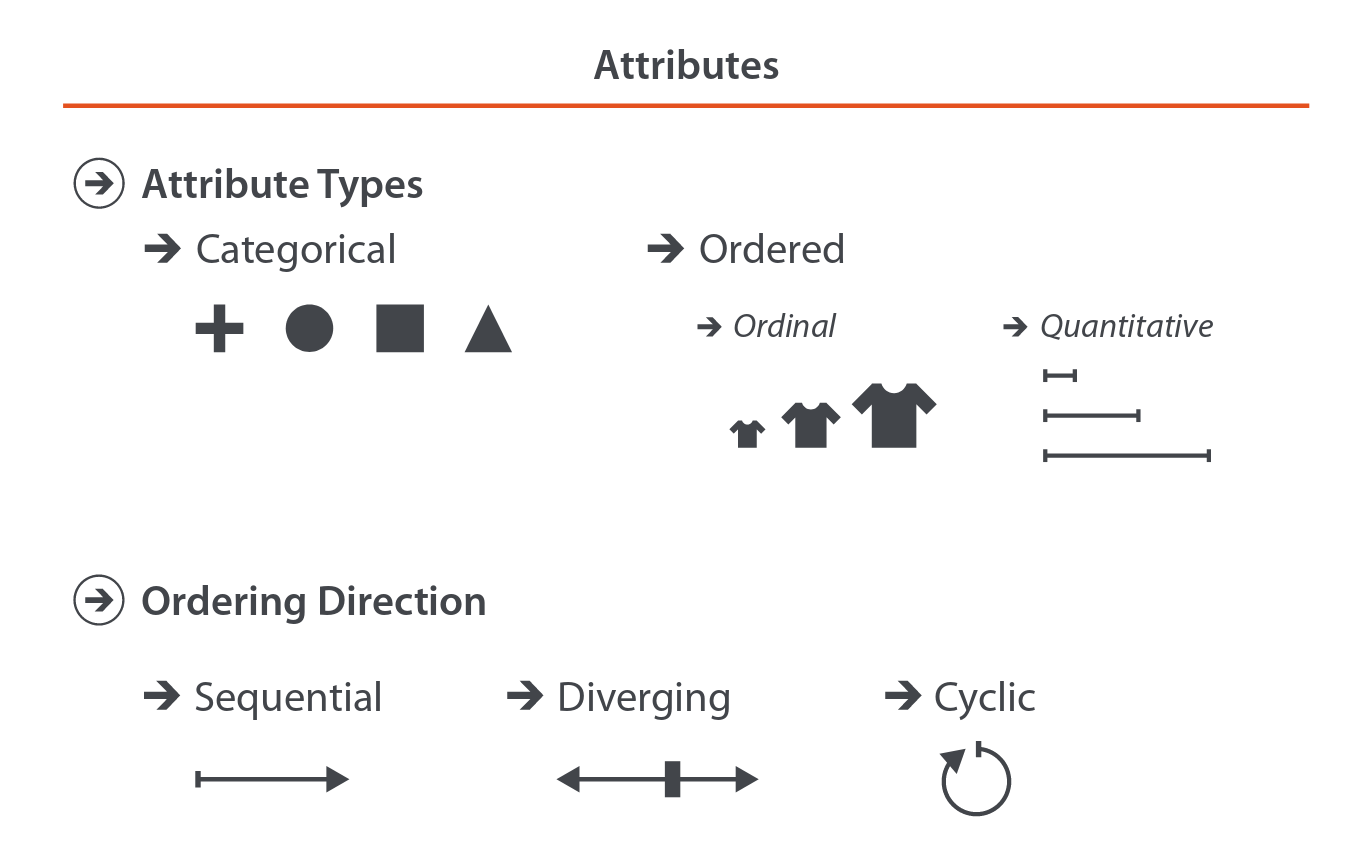
Observamos que los atributos tienen dos características: tipo y dirección.

Los tipos de atributo definidos son los siguientes:

• Categóricos: el valor del atributo define la pertenencia o asociación a un grupo, una categoría. En estos grupos no existe relación natural de orden. Ejemplos: ¿Perro o Gato?¿Colo Colo o Universidad de Chile?¿Cuadrado, Círculo o Triángulo?
• Ordinales: el valor del atributo define la pertenencia o asociación a un grupo o categoría en los que sí existe un orden natural. Por ejemplo, las tallas de poleras son atributos ordinales: S < M < L < XL. La existencia de orden no implica que se puedan realizar operaciones artiméticas con ellos. Por mucho que yo quisiera, no existe la talla media entre M y L.s
• Cuantitativos: el valor del atributo pertenece a un espacio numérico, donde existe orden entre distintos números (se pueden comparar) y también se pueden realizar operaciones aritméticas (+, -, *, /). Generalmente es un número entero o un número real.

Las direcciones que pueden tomar los atributos cuantitativos son las siguientes:

• Secuencial: El valor del atributo se define respecto a un punto de origen, y desde ese punto solamente se puede avanzar en una dirección. Un ejemplo de esto es la edad: el valor inicial es 0, y solamente puede incrementar. No existen personas con edades negativas.
• Divergente: El valor del atributo se define respecto a un punto de origen, y desde ese punto se puede avanzar en direcciones opuestas. Un ejemplo es la temperatura en grados Celsius, donde el punto de referencia es 0° (punto de congelación del agua), y hay temperaturas negativas y positivas.
• Cíclico: El valor del atributo se define respecto a un punto de origen, y desde ese punto se puede avanzar en dirección positiva o negativa, pero con ciclos — después de avanzar una cierta cantidad, se vuelve al punto de origen. Un ejemplo son los meses del año.

Veremos más adelante que el rol de esta caracterización de atributos es importante a la hora de determinar las codificaciones visuales.

Ejemplo: Fechas y Atributos Cíclicos #

La fecha es un atributo interesante, puesto que puede ser interpretada de múltiples maneras. Por un lado, si se considera un punto de partida, es secuencial. Las fechas comunes del calendario gregoriano son divergentes, puesto que se definen a partir de una fecha de referencia. Si consideramos los meses del año, éstos son cíclicos, puesto que a pesar de que existe un orden entre ellos. Sabemos que Enero < Abril < Septiembre, también sabemos que existe la transición Diciembre -> Enero.

La siguiente visualización es un ejemplo del tratamiento de fechas. Muestra el cambio en la temperatura global en los últimos 170 años:

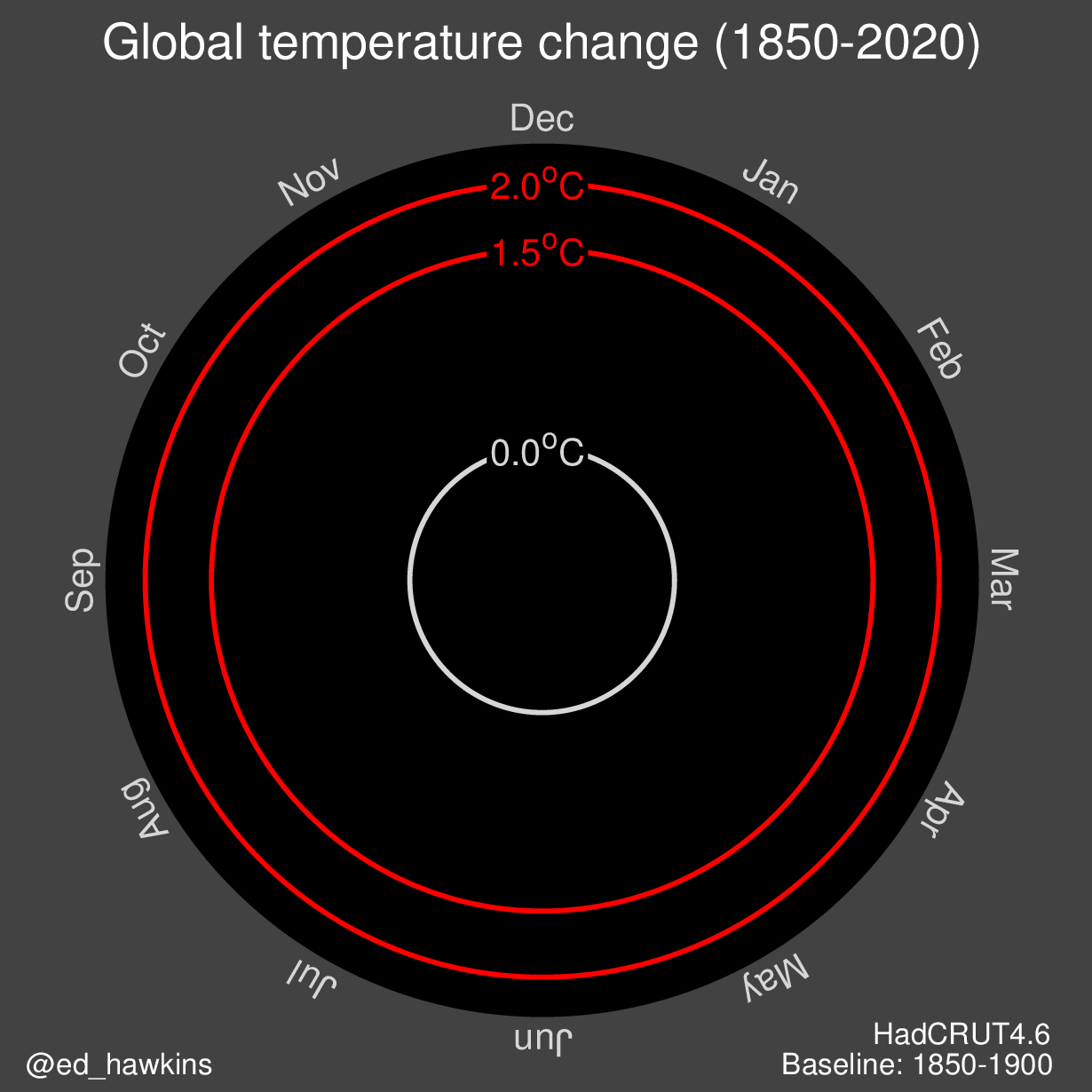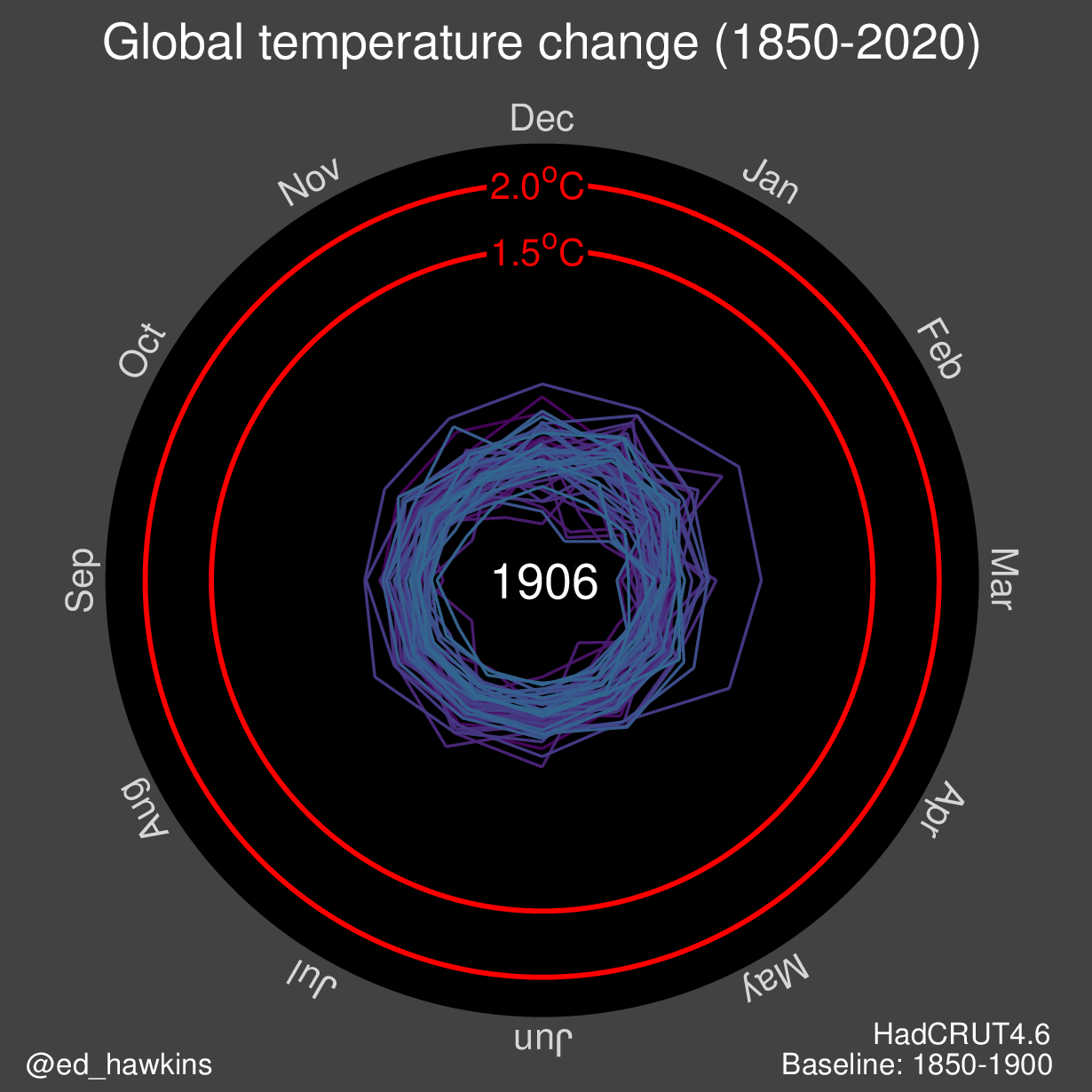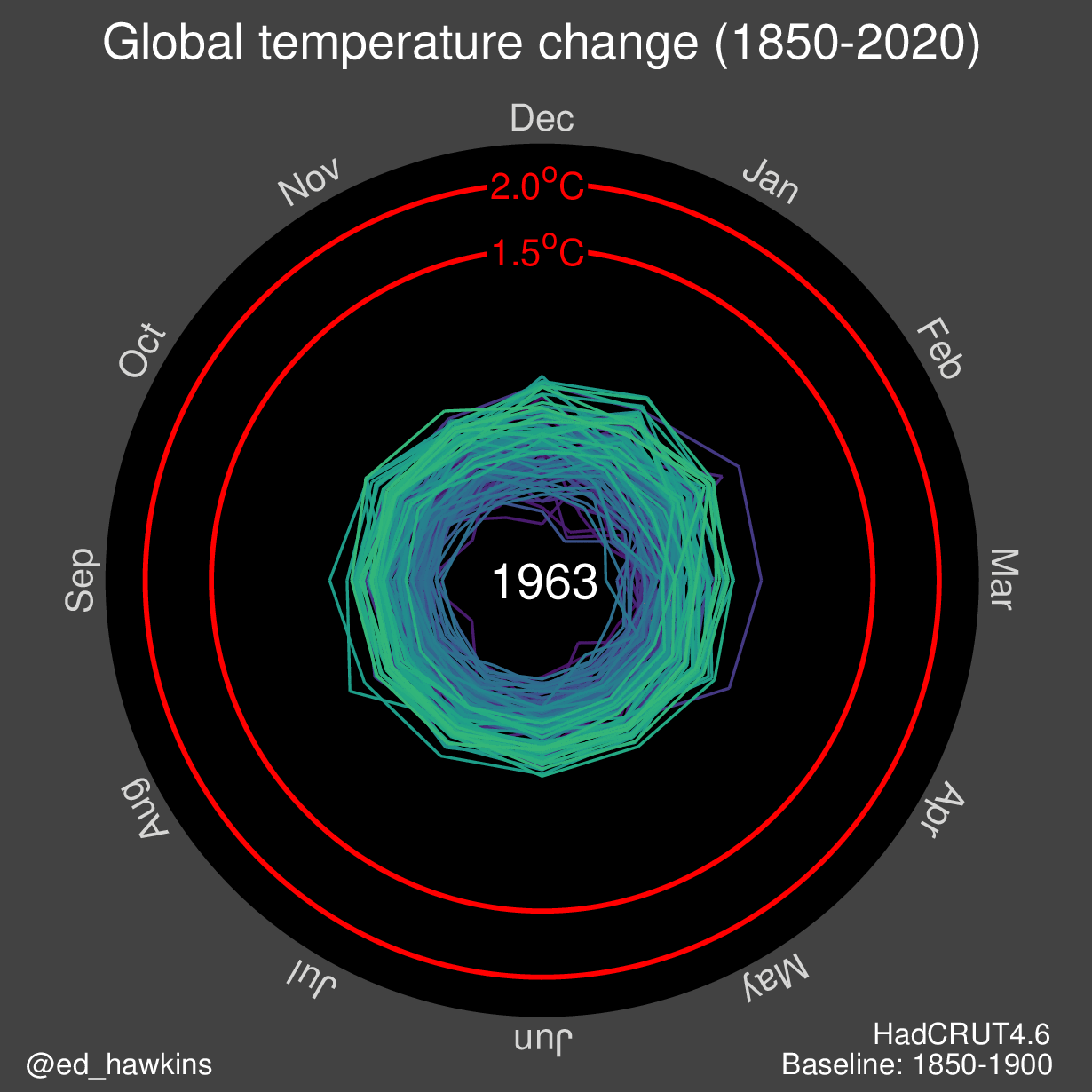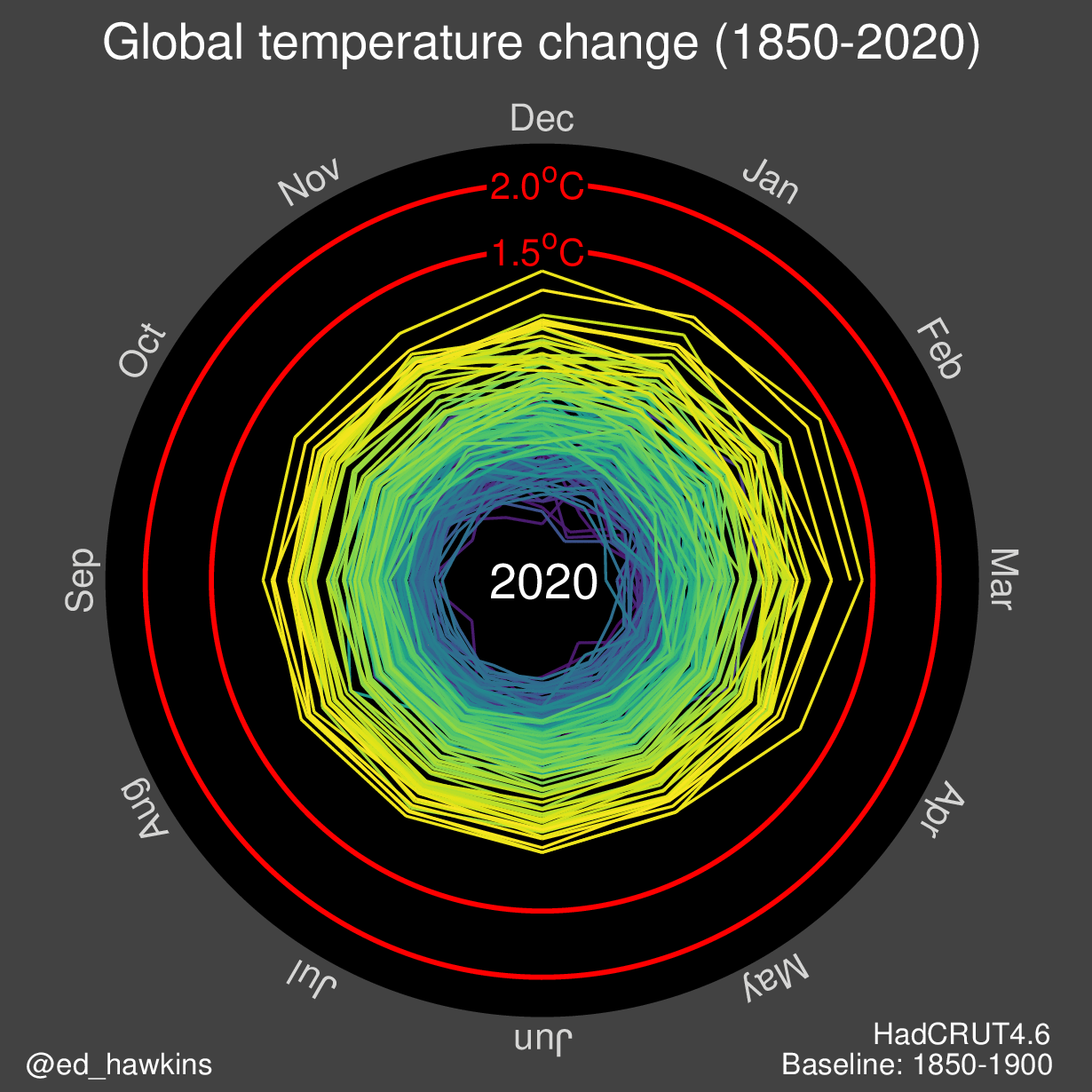
Este gráfico particular utiliza coordenadas polares para representar los ciclos.

Conclusiones #

En esta unidad hemos visto como podemos abstraer los datos (lo que vamos a visualizar) a través de una definición de tipos de datasets y de los atributos que tienen los elementos que conforman estos datasets.

Los datos son la piedra fundamental de la visualización tal como la hemos definido. Llegar a una solución efectiva para el problema que queremos resolver será posible solo en caso de entender los datos que tenemos y su pertinencia para el problema.

Un aspecto que no veremos en el curso, por ser más propio de un curso de análisis de datos, es la limpieza de éstos. Usualmente los datos requieren tratamientos para sacar ruido, inconsistencias, registros inválidos, registros incompletos, etc. En nuestro curso asumiremos que ese proceso ya ha sucedido, sin perjuicio de que la visualización es una herramienta útil en determinar el estado de un dataset.

Para terminar, a modo de fomentar reflexiones futuras, existe una cita que es usada frecuentemente en ciencia de datos y estadística:

Sin datos, eres simplemente otra persona opinando.

– W. Edwards Deming

Esta afirmación es potente, porque si tenemos datos y queremos utilizarlos como respaldo en nuestras decisiones, debemos ser capaces de comunicarlos. Al mismo tiempo, no pone en duda la veracidad o la completitud de éstos. Hay otras preguntas que es necesario realizar para un dataset: ¿quién genera los datos?¿con qué propósito?¿qué tan representativos son? El tema de sesgo en los datos (y otros sesgos) es relevante hoy. Sin embargo, su discusión está fuera del alcance de este curso, a pesar de que la visualización es una herramienta que permite indagar en estos aspectos.